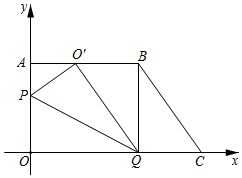
如图,在平面直角坐标系中,四边形的边在轴上,在轴上.为坐标原点,,线段,的长分别是方程的两个根,.
(1)求点,的坐标;
(2)为上一点,为上一点,,将翻折,使点落在上的点处,双曲线的一个分支过点.求的值;
(3)在(2)的条件下,为坐标轴上一点,在平面内是否存在点,使以,,,为顶点四边形为矩形?若存在,请直接写出点的坐标;若不存在,请说明理由.
推荐套卷
如图,在平面直角坐标系中,四边形的边在轴上,在轴上.为坐标原点,,线段,的长分别是方程的两个根,.
(1)求点,的坐标;
(2)为上一点,为上一点,,将翻折,使点落在上的点处,双曲线的一个分支过点.求的值;
(3)在(2)的条件下,为坐标轴上一点,在平面内是否存在点,使以,,,为顶点四边形为矩形?若存在,请直接写出点的坐标;若不存在,请说明理由.
