已知双曲线y= (k>0,x>0)与矩形ABCD,A(2,1)C(6,4)设双曲线与折线A-D-C交于E,与折线A-B-C交于F.
(k>0,x>0)与矩形ABCD,A(2,1)C(6,4)设双曲线与折线A-D-C交于E,与折线A-B-C交于F.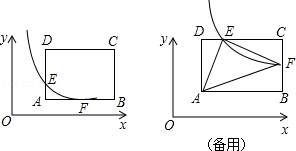
(1)写出B,D两点的坐标;
(2)k为何值时,双曲线与矩形有公共点;
(3)设△AEF的面积为y,当E,F分别在DC和BC上时,确定y与k之间的函数关系式,并确定k取值范围;
(4)当E,F分别在DC和BC上,且△AEF为直角三角形,求k的值;
(5)直接写出EF的最大值.
如图1,在平面直角坐标系中,O为坐标原点,直线y=-2x+5与x轴、y轴分别交于C、D两点,与双曲线y=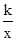 (k≠0,x>0)交于A、B两点.
(k≠0,x>0)交于A、B两点.
(1)若B点的横坐标为2,求k的值.
(2)设A点的横坐标为m,B点的横坐标为n,求m与n之间的函数关系式(不要求写出自变量的取值范围)
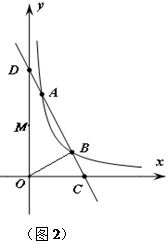
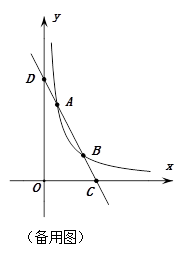
(3)如图2连结BO,取DO中点M,当以MO、BO、AD的长为三边构成的三角形的面积为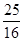 时,在y=
时,在y=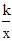 (k≠0,x>0)的图象上是否存在一点E,连接CE,BE,使得△BCE是以C为直角顶点的等腰直角三角形.若存在,求E点坐标,若不存在,请说明理由.
(k≠0,x>0)的图象上是否存在一点E,连接CE,BE,使得△BCE是以C为直角顶点的等腰直角三角形.若存在,求E点坐标,若不存在,请说明理由.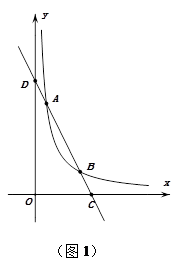
如图,在平面直角坐标系中,四边形ABCD是菱形,B、O在x轴负半轴上,AO=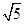 ,tan∠AOB=
,tan∠AOB=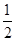 ,一次函数
,一次函数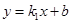 的图象过A、B两点,反比例函数
的图象过A、B两点,反比例函数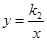 的图象过OA的中点D.
的图象过OA的中点D.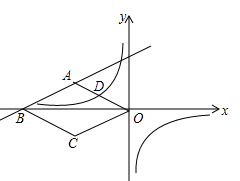
(1)求一次函数和反比例函数的表达式;
(2)平移一次函数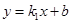 的图象,当一次函数
的图象,当一次函数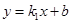 的图象与反比例函数
的图象与反比例函数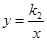 的图象无交点时,求b的取值范围.
的图象无交点时,求b的取值范围.
(本小题满分9分)如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(-2,0)、B(0,d)、C(-3,2).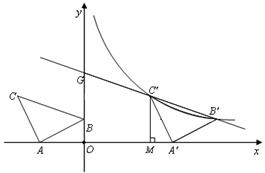
(1)求d的值;
(2)将△ABC沿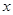 轴的正方向平移a个单位,在第一象限内B、C两点的对应点B′、C′正好落在某反比例函数图像上.请求出这个反比例函数和此时直线
轴的正方向平移a个单位,在第一象限内B、C两点的对应点B′、C′正好落在某反比例函数图像上.请求出这个反比例函数和此时直线 的解析式;
的解析式;
(3)在(2)的条件下,直线 交y轴于点G,作
交y轴于点G,作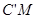 ⊥
⊥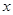 轴于
轴于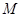 .
.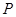 是线段
是线段 上的一点,若△
上的一点,若△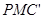 和△
和△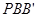 面积相等,求点
面积相等,求点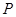 坐标.
坐标.
(黄石)已知双曲线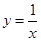 (
(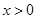 ),直线
),直线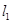 :
: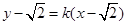 (
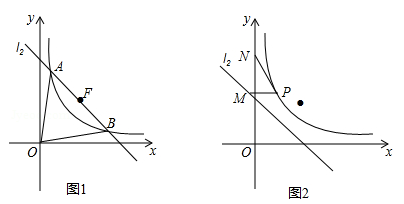
(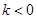 k<0)过定点F且与双曲线交于A,B两点,设A(
k<0)过定点F且与双曲线交于A,B两点,设A(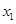 ,
,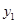 ),B(
),B(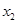 ,
, )(
)(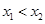 ),直线
),直线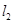 :
: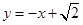 .
.
(1)若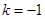 ,求△OAB的面积S;
,求△OAB的面积S;
(2)若AB=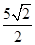 ,求k的值;
,求k的值;
(3)设N(0,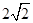 ),P在双曲线上,M在直线l2上且PM∥x轴,求PM+PN最小值,并求PM+PN取得最小值时P的坐标.(参考公式:在平面直角坐标系中,若A(
),P在双曲线上,M在直线l2上且PM∥x轴,求PM+PN最小值,并求PM+PN取得最小值时P的坐标.(参考公式:在平面直角坐标系中,若A(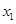 ,
,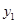 ),B(
),B(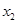 ,
, )则A,B两点间的距离为AB=
)则A,B两点间的距离为AB=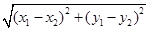 .
.
如图,ABMN中,AC平分∠BAN交BM于C点,CD∥AB交AN于D点.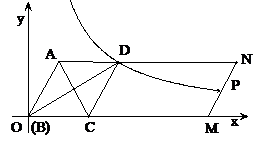
(1)判断四边形ABCD的形状并证明你的结论;
(2)以B点为坐标原点,BM所在的直线为横轴建立平面直角坐标系,若∠ABM = 60°,A点横坐标为2,请直接写出A、C、D点坐标及经过D点的反比例函数解析式;
(3)设(2)中反比例函数的图象与MN交于P点,求当BM的长为多少时,P点为MN的中点。
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标(4,2),过点D(0,3)和E(6,0)的直线分别于AB,BC交于点M,N.
(1)求直线DE的解析式和点M的坐标;
(2)若反比例函数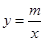 (x>0)的图象经过点M,求该反比函数的解析式,并通过计算判断点N是否在该函数的图象上.
(x>0)的图象经过点M,求该反比函数的解析式,并通过计算判断点N是否在该函数的图象上.
如图(1),直线y=k1 x+b与反比例函数y=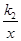 的图象交于点A(1,6),B(a,3)两点.
的图象交于点A(1,6),B(a,3)两点.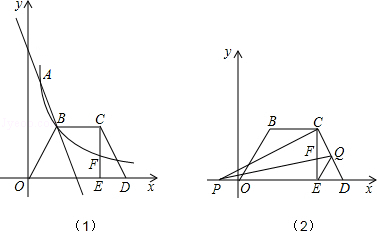
(1)求k1、k2的值;
(2)如图(1),等腰梯形OBCD中,BC∥OD,OB=CD,OD边在x轴上,过点C作CE⊥OD于点E,CE和反比例函数的图象交于点F,当梯形OBCD的面积为12时,请判断FC和EF的大小,并说明理由;
(3)如图(2),已知点Q是CD的中点,在第(2)问的条件下,点P在x轴上,从原点O出发,沿x轴负方向运动,设四边形PCQE的面积为S1,△DEQ的面积为S2,当∠PCD=90°时,求P点坐标及S1:S2的值.
平行四边形ABCD在平面直角坐标系中的位置如图所示,其中A(-6,0),B(4,0),C(5,3),反比例函数y= 的图象经过点C.
的图象经过点C.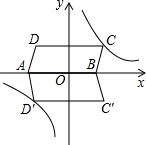
(1)求此反比例函数的解析式;
(2)将平行四边形ABCD沿x轴翻折得到平行四边形AD′C′B,请你通过计算说明点D′在双曲线上;
(3)请你画出△AD′C,并求出它的面积.
(1)如图1,已知△ABC三个顶点的坐标分别为A(1,4)、B(4,1)、C(4,4),若双曲线y= (x>0)与△ABC有公共点,则k的取值范围是 ;
(x>0)与△ABC有公共点,则k的取值范围是 ;
(2)把图1中的△ABC沿直线AB翻折后得到△ABC1,若双曲线y=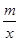 (x>0)与△ABC1有公共点,求m的取值范围;
(x>0)与△ABC1有公共点,求m的取值范围;
小明借助一元二次方程根的判断式圆满地解决了这个问题,小芳借助二次函数模型也圆满地解决了这个问题.请你先在图2中画出△ABC1,再写出自己的解答过程.
(3)如图3,已知点A为(1,2),点B为(4,1),若双曲线y= (x>0)与线段AB有公共点,则n的取值范围是 .
(x>0)与线段AB有公共点,则n的取值范围是 .
在数学兴趣小组活动中,小亮进行数学探究活动. 是边长为2的等边三角形, 是 上一点,小亮以 为边向 的右侧作等边三角形 ,连接 .
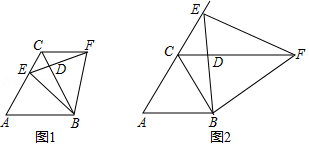
(1)如图1,当点 在线段 上时, 、 相交于点 ,小亮发现有两个三角形全等,请你找出来,并证明.
(2)当点 在线段 上运动时,点 也随着运动,若四边形 的面积为 ,求 的长.
(3)如图2,当点 在 的延长线上运动时, 、 相交于点 ,请你探求 的面积 与 的面积 之间的数量关系.并说明理由.
(4)如图2,当 的面积 时,求 的长.
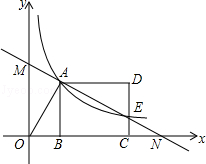
如图,反比例函数y= (x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(2,0),tan∠AOB=
(x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(2,0),tan∠AOB=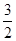 .
.
(1)求k的值;
(2)将线段AB沿x轴正方向平移到线段DC的位置,反比例函数y= (x>0)的图象恰好经过DC上一点E,且DE:EC=2:1,求直线AE的函数表达式;
(x>0)的图象恰好经过DC上一点E,且DE:EC=2:1,求直线AE的函数表达式;
(3)若直线AE与x轴交于点,N,与y轴交于点M,请你探索线段AM与线段NE的大小关系,写出你的结论并说明理由.
有一个 ,
, ,
,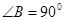 ,
, ,将它放在直角坐标系中,使斜边
,将它放在直角坐标系中,使斜边 在
在 轴上,直角顶点
轴上,直角顶点 在反比例函数
在反比例函数 的图象上,求点
的图象上,求点 的坐标.
的坐标.
如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(-2,0)、
B(0,1)、C(d,2)。
(1)求d的值;
(2)将△ABC沿x轴的正方向平移,在第一象限内B、C两点的对应点B′、C′正好落在某反比例函数图
像上。请求出这个反比例函数和此时的直线B′C′的解析式;
(3)在(2)的条件下,直线B′C′交y轴于点G。问是否存在x轴上的点M和反比例函数图像上的点P,
使得四边形PGMC′是平行四边形。如果存在,请求出点M和点P的坐标;如果不存在,请说明理由。