初中数学平行线分线段成比例解答题

（1）如图1，已知△ABC三个顶点的坐标分别为A（1，4）、B（4，1）、C（4，4），若双曲线y=（x＞0）与△ABC有公共点，则k的取值范围是 ；
（2）把图1中的△ABC沿直线AB翻折后得到△ABC₁，若双曲线y=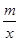（x＞0）与△ABC₁有公共点，求m的取值范围；
小明借助一元二次方程根的判断式圆满地解决了这个问题，小芳借助二次函数模型也圆满地解决了这个问题．请你先在图2中画出△ABC₁，再写出自己的解答过程．
（3）如图3，已知点A为（1，2），点B为（4，1），若双曲线y=（x＞0）与线段AB有公共点，则n的取值范围是 ．

如图，正方形ABCO的顶点A，C分别在x轴，y轴上，O为坐标原点，点B在第二象限，边长为m，双曲线线y=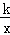（x≠0）经过BC的中点H．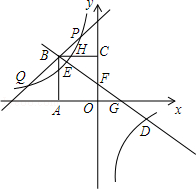

（1）用m的代数式表示出k；
（2）当m=3时，过B作直线BD，分别交x轴，y轴于G、F，分别交双曲线线y=（x≠0）的两个分支于E、D，求证：GE=DF；
（3）在（2）的前提下，将直线BD绕点B旋转适当的角度在第二象限与双曲线线y=（x≠0）交于P、Q，分别过P、Q作直线AC的垂线PM、QN，垂足为M、N，试探究PQ与PM+QN的数量关系并证明．

（本小题满分12分）
如图①，O为坐标原点，点B在x轴的正半轴上，四边形OACB是平行四边形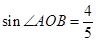，，反比例函数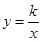（k＞0）在第一象限内的图象经过点A，与BC交于点F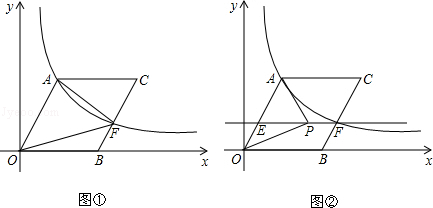

（1）若OA=10，求反比例函数解析式；
（2）若点F为BC的中点，且△AOF的面积S=12，求OA的长和点C的坐标；
（3）在（2）中的条件下，过点F作EF∥OB，交OA于点E（如图②），点P为直线EF上的一个动点，连接PA，PO 是否存在这样的点P，使以P、O、A为顶点的三角形是直角三角形？若存在，请直接写出所有点P的坐标；若不存在，请说明理由

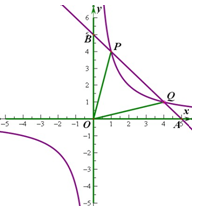
如图，已知反比例函数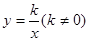的图象经过点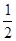（，8），直线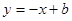经过该反比例函数图象上的点Q（4，）．

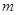（1）求上述反比例函数和直线的函数表达式；
（2）设该直线与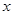轴、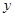轴分别相交于A 、B两点，与反比例函数图象的另一个交点为P，连结0P、OQ，求△OPQ的面积．

如图， $\mathit{\Delta ABC}$中， $\mathit{AB}=\mathit{AC}$， $\odot O$是 $\mathit{\Delta ABC}$的外接圆， $\mathit{BO}$的延长线交边 $\mathit{AC}$于点 $D$．

[小题1]求证： $\angle \mathit{BAC}=2\angle \mathit{ABD}$；

[小题2]当 $\mathit{\Delta BCD}$是等腰三角形时，求 $\angle \mathit{BCD}$的大小；

[小题3]当 $\mathit{AD}=2$， $\mathit{CD}=3$时，求边 $\mathit{BC}$的长．

（本小题满分10分）某商店第一次用600元购进某种铅笔若干支，第二次又用600元购进该种铅笔，但这次每支的进价比第一次贵l元，所以购进数量比第一次少了30支．
（1）求第一次每支铅笔的进价及购进的数量；
（2）若将这两次购进的铅笔按同一单价x（元，支）全部销售完毕，并要求获利不低于420元，求获利y（元）关于单价x（元／支）的函数关系式及定义域，并在直角坐标系内画出它的大致图象．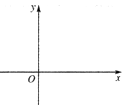

一次函数y=ax+b与反比例函数的图象交于A、B两点．过A点分别作x轴、y 轴的垂线，E、F为垂足．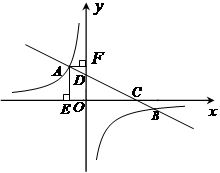

（1）请直接写出矩形AEOF的面积；
（2）设一次函数y=ax+b与x轴、y轴的交点分别为C、D，当OC=3OE时．
①试求△OCD的面积；
②当OE=1时，以BD为直径作⊙N，与x轴相交于P点，请求出P点的坐标．

如图，正方形AOCB在平面直角坐标系xoy中，点O为原点，点B在反比例函数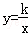（x＞0）图象上，△BOC的面积为8．

（1）求反比例函数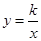的关系
（2）若动点E从A开始沿AB向B以每秒1个单位的速度运动，同时动点F从B开始沿BC向C以每秒2个单位的速度运动，当其中一个动点到达端点时，另一个动点随之停止运动．若运动时间用t表示，△BEF的面积用S表示，求出S关于t的函数关系式？
（3）当运动时间为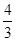秒时，在坐标轴上是否存在点P，使△PEF的周长最小？若存在，请求出点P的坐标；若不存在，请说明理由．

如图，四边形ABCD为正方形，点A的坐标为（0，2），点B的坐标为（0，-3），反比例函数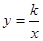的图象经过点C，一次函数y=ax+b的图象经过点A.C

（1）求反比例函数和一次函数的解析式
（2）若点P是反比例函数图象上的一点，△OAP的面积恰好等于正方形ABCD的面积，请直接写出P点的坐标.

如图，点A是反比例函数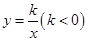图像上的一点，过点A作AB⊥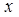轴于点B，且△AOB的面积为2，点A的坐标为．

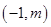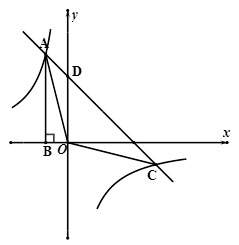
（1）求m和k的值．
（2）若一次函数y=ax+3的图像经过点A，交双曲线的另一支于点C，交y轴于点D，求△AOC的面积．
（3）在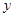轴上是否存在点P，使得△PAC的面积为6？如果存在，请求出点P的坐标；若不存在，请说明理由．

如图，一次函数y₁=mx+n的图象与x轴、y轴分别交于A、B两点，与反比例函数y₂=（x＜0）交于点C，过点C分别作x轴、y轴的垂线，垂足分别为点E、F．若OB=2，CF=6，．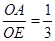

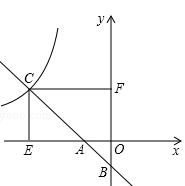
（1）求点A的坐标；
（2）求一次函数和反比例函数的表达式．

如图，反比例函数y=（x＞0）的图象经过线段OA的端点A，O为原点，作AB⊥x轴于点B，点B的坐标为（2，0），tan∠AOB=．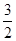

（1）求k的值；
（2）将线段AB沿x轴正方向平移到线段DC的位置，反比例函数y=（x＞0）的图象恰好经过DC上一点E，且DE：EC=2：1，求直线AE的函数表达式；
（3）若直线AE与x轴交于点，N，与y轴交于点M，请你探索线段AM与线段NE的大小关系，写出你的结论并说明理由．

近年来，我国煤矿安全事故频频发生，其中危害最大的是瓦斯，其主要成分是CO．在一次矿难事件的调查中发现：从零时起，井内空气中CO的浓度达到4mg/L，此后浓度呈直线型增加，在第7小时达到最高值46mg/L，发生爆炸；爆炸后，空气中的CO浓度成反比例下降．如图所示，根据题中相关信息回答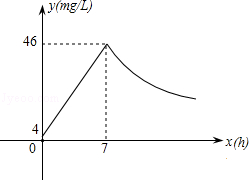

下列问题：
（1）求爆炸前后空气中CO浓度y与时间x的函数关系式，并写出相应的自变量取值范围；
（2）当空气中的CO浓度达到34mg/L时，井下3km的矿工接到自动报警信号，这时他们至少要以多少km/h的速度撤离才能在爆炸前逃生？
（3）矿工只有在空气中的CO浓度降到4mg/L及以下时，才能回到矿井开展生产自救，求矿工至少在爆炸后多少小时才能下井？

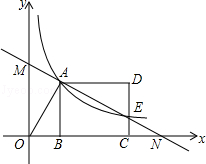
如图，在平面直角坐标系中，直线l与x轴相交于点M，与y轴相交于点N，Rt△MON的外心为点A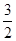（，-2），反比例函数y=（x＞0）的图象过点A．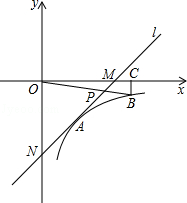

（1）求直线l的解析式；
（2）在函数y=（x＞0）的图象上取异于点A的一点B，作BC⊥x轴于点C，连接OB交直线l于点P．若△ONP的面积是△OBC面积的3倍，求点P的坐标．

如图，反比例函数与一次函数的图象交于两点A(1,3)、B(n，-1)．

（1）求这两个函数的解析式；
（2）观察图象，请直接写出不等式的解集；
（3）点C为x轴正半轴上一点，连接AO、AC，且AO=AC,求⊿AOC的面积．