在边长为1的4×4方格上建立直角坐标系(如图甲),在第一象限内画出反比例函数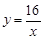 、
、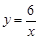 、
、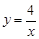 的图象,它们分别经过方格中的一个格点、二个格点、三个格点;在边长为1的10×10方格上建立直角坐标系(如图乙),在第一象限内画出反比例函数的图象,使它们经过方格中的三个或四个格点,则最多可画出几条 ( )
的图象,它们分别经过方格中的一个格点、二个格点、三个格点;在边长为1的10×10方格上建立直角坐标系(如图乙),在第一象限内画出反比例函数的图象,使它们经过方格中的三个或四个格点,则最多可画出几条 ( )
| A.12 | B.13 | C.25 | D.50 |

如图,在x轴正半轴上依次截取OA1=A1A2=A2A…An-1An(n为正整数),过点A1、A2、A3、…、An分别作x轴的垂线,与反比例函数y=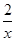 (x>0)交于点P1、P2、P3、…、Pn,连接P1P2、P2P3、…、Pn-1Pn,过点P2、P3、…、Pn分别向P1A1、P2A2、…、Pn-1An-1作垂线段,构成的一系列直角三角形(见图中阴影部分)的面积和是 ()
(x>0)交于点P1、P2、P3、…、Pn,连接P1P2、P2P3、…、Pn-1Pn,过点P2、P3、…、Pn分别向P1A1、P2A2、…、Pn-1An-1作垂线段,构成的一系列直角三角形(见图中阴影部分)的面积和是 ()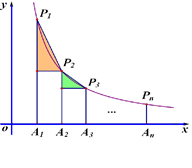
A.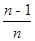 |
B.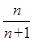 |
C.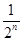 |
D.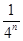 |
如图,Rt△OAB的顶点O与坐标原点重合,∠AOB=90°,AO=2BO,当A点在反比例函数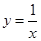 (x>0)的图象上移动时,B点坐标满足的反比例函数解析式为
(x>0)的图象上移动时,B点坐标满足的反比例函数解析式为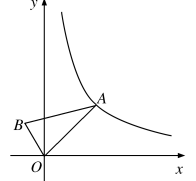
A.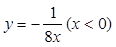 |
B.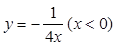 |
C.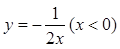 |
D.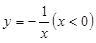 |
已知正比例函数y1=x,反比例函数y2=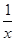 ,由y1,y2构造一个新函数y=x+
,由y1,y2构造一个新函数y=x+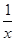 ,其图象如图所示.(因其图象似双钩,我们称之为“双钩函数”).给出下列几个命题:
,其图象如图所示.(因其图象似双钩,我们称之为“双钩函数”).给出下列几个命题:
①该函数的图象是中心对称图形;
②当x<0时,该函数在x=-1时取得最大值-2;
③y的值不可能为1;
④在每个象限内,函数值y随自变量x的增大而增大.
其中正确的命题是()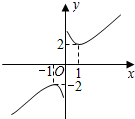
| A.①②④ | B.①②③ | C.②③ | D.①③ |
如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m,3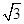 ),反比例函数
),反比例函数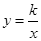 的图像与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是()
的图像与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是()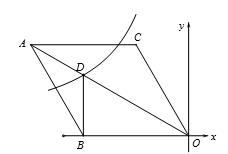
A.6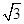 |
B.-6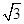 |
C.12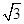 |
D.-12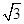 |
如图所示,已知A(  ,
,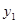 ),B(2,
),B(2,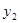 )为反比例函数
)为反比例函数 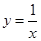 图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是()
图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是()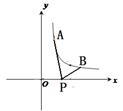
A.(  ,0) ,0) |
B.(1,0) | C.(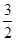 ,0) ,0) |
D.(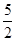 ,0) ,0) |
如图,直线 与反比例函数
与反比例函数 的图象在第一象限内交于A、B两点,交x轴的正半轴于C点,若AB:BC=(m-1):1(m>1),则△OAB的面积(用m表示)为()
的图象在第一象限内交于A、B两点,交x轴的正半轴于C点,若AB:BC=(m-1):1(m>1),则△OAB的面积(用m表示)为()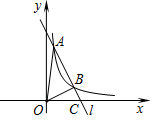
A.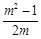 B.
B.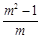 C.
C.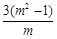 D.
D.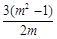
如图,OABC是平行四边形,对角线OB在y轴正半轴上,位于第一象限的点A和第二象限的点C分别在双曲线y=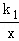 和y=
和y= 的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:①
的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:①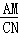 =
=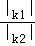 ;②阴影部分面积是
;②阴影部分面积是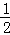 (k1+k2);③当∠AOC=90°时,|k1|=|k2|;④若OABC是菱形,则两双曲线既关于x轴对称,也关于y轴对称.其中正确的结论是()
(k1+k2);③当∠AOC=90°时,|k1|=|k2|;④若OABC是菱形,则两双曲线既关于x轴对称,也关于y轴对称.其中正确的结论是()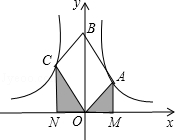
A.①②③ B.②④ C.①③④ D.①④
已知n是正整数,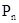 (
(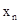 ,
,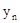 )是反比例函数
)是反比例函数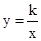 图象上的一列点,其中
图象上的一列点,其中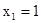 ,
,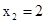 ,…,
,…,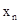 =n; 记
=n; 记 ,
,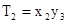 ,…,
,…,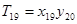 ;若
;若 ,则
,则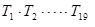 的值是()
的值是()
| A.0.1×218 | B.0.1×219 |
| C.0.1×220 | D.0.1×221 |
如图,等边三角形OAB的一边OA在x轴上,双曲线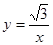
 在第一象限内的图像经过OB边的中点C,则点B的坐标是()
在第一象限内的图像经过OB边的中点C,则点B的坐标是()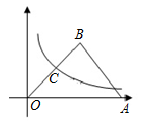
A.( 1,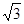 ) ) |
B.(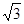 ,1 ) ,1 ) |
C.( 2,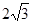 ) ) |
D.(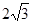 ,2 ) ,2 ) |
已知反比例函数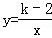 的图象如图,则一元二次方程x2﹣(2k﹣1)x+k2﹣1=0根的情况是()
的图象如图,则一元二次方程x2﹣(2k﹣1)x+k2﹣1=0根的情况是()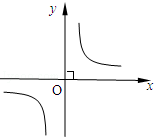
| A.有两个不等实根 |
| B.有两个相等实根 |
| C.没有实根 |
| D.无法确定 |
如图,直线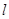 和双曲线
和双曲线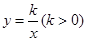 交于
交于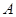 ,
,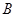 两点,
两点,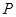 是线段
是线段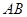 上的点(不与
上的点(不与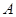 ,
,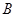 重合),过点
重合),过点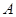 ,
,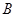 ,
,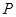 分别向
分别向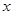 轴作垂线,垂足分别是
轴作垂线,垂足分别是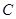 ,
, 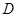 ,
,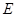 ,连接
,连接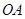 ,
,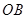 ,
,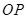 ,设
,设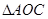 面积是
面积是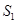 ,
,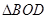 面积是
面积是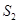 ,
,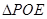 面积是
面积是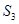 ,则().
,则().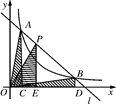
A.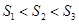 |
B.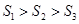 |
C.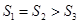 |
D. |
如图,每个底边为2的等腰三角形顶角的顶点都在反比例函数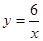 (x>0)的图像上,第1个等腰三角形顶角的顶点横坐标为1,第2个等腰三角形的顶点横坐标为3,……以此类推,用含n的式子表示第n个等腰三角形底边上的高为()
(x>0)的图像上,第1个等腰三角形顶角的顶点横坐标为1,第2个等腰三角形的顶点横坐标为3,……以此类推,用含n的式子表示第n个等腰三角形底边上的高为()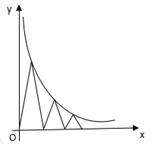
A.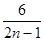 |
B.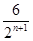 |
C. |
D.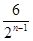 |
如图,直线x=t(t>0)与反比例函数y=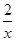 ,y=
,y=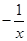 的图象分别交于B,C两点,A为y轴上的任意一点,则△ABC的面积为()
的图象分别交于B,C两点,A为y轴上的任意一点,则△ABC的面积为()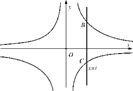
| A.3 | B.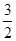 t t |
C.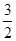 |
D.不能确定 |