江苏省无锡市洛社初级中学八年级下学期期中考试数学试卷
矩形具有而菱形不一定具有的性质是 ( )
| A.对角线互相垂直 | B.对角线相等 | C.对角线互相平分 | D.对角互补 |
在平行四边形ABCD中,对角线AC、BD相交于点O,如果AC=10,BD=8,AB=x,则x的取值范围是 ( )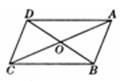
A.1<x<9 B.2<x<18 C.8<x<10 D.4<x<5
下列关于x的一元二次方程中,有两个不相等的实数根的方程是( )
| A.x2+4=0 | B.4x2-4x+1=0 |
| C.x2+x+3=0 | D.x2+2x-1=0 |
某市为发展教育事业,加强了对教育经费的投入,2013年投入3000万元,预计2015年投入5000万元.设教育经费的年平均增长率为 ,根据题意,下面所列方程正确的是 ……( )
,根据题意,下面所列方程正确的是 ……( )
A. |
B. |
C. |
D.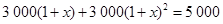 |
函数 的图象经过点A(6,-1),则下列点中不在该函数图象上的点是 ( )
的图象经过点A(6,-1),则下列点中不在该函数图象上的点是 ( )
| A.(-2,3) | B.(-1,-6) | C.(1,-6) | D.(2,-3) |
某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P ( kPa )是气体体积V ( m3)的反比例函数,其图象如图所示.当气球内的气压大于120 kPa时,气球将爆炸.为了安全起见,气球的体积应( )
A.不小于 m3 m3 |
B.小于 m3 m3 |
C.不小于 m3 m3 |
D.小于 m3 m3 |
如图,P为平行四边形ABCD内一点,过点P分别作AB、AD的平行线交平行四边形于E、F、G、H四点,若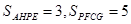 ,则
,则 为 ( )
为 ( )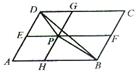
A.0.5 B.1 C.1.5 D.2
如图所示,已知A(  ,
,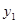 ),B(2,
),B(2,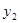 )为反比例函数
)为反比例函数 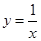 图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )
图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )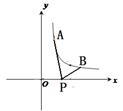
A.(  ,0) ,0) |
B.(1,0) | C.(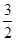 ,0) ,0) |
D.(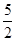 ,0) ,0) |
设x1,x2是方程2x2-6x+3=0的两根,则x1+x2=______,x1·x2= .
已知y与2x+1成反比例,且当x=1时,y=2,那么当x=-2时,y=______.
关于x的一元二次方程(m-2)x2+3x+m2-4=0有一解为0,则m的值是 .
在菱形ABCD中,已知AB=10,AC=16,那么菱形ABCD的面积为_______.
如图,平行四边形ABCD中,点E在边AD上,以BE为折痕,将△ABE折叠,使点A正好与CD上的F点重合,若△FDE的周长为16,△FCB的周长为28,则FC的长为 .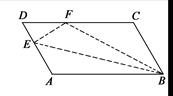
若函数y= 的图象在第二、四象限,则函数y=kx-1的图象经过第_____象限.
的图象在第二、四象限,则函数y=kx-1的图象经过第_____象限.
如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为 .
如图,在平面直角坐标系中,A(1,0),B(0,3),以AB为边在第一象限作正方形ABCD,点D在双曲线y= (k≠0)上,将正方形沿x轴负方向平移 m个单位长度后,点C恰好落在双曲线上,则m的值是 .
(k≠0)上,将正方形沿x轴负方向平移 m个单位长度后,点C恰好落在双曲线上,则m的值是 .
解方程组(每题4分,共16分)
(1)x2-5x-6=0
(2)3x2-4x-1=0;
(3)x(x-1)=3-3x;
(4)x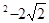 x+1=0
x+1=0
(本题8分)如图,在 中,E、F为对角线BD上的两点.
中,E、F为对角线BD上的两点.
(1)若AE⊥BD,CF⊥BD,证明BE=DF.
(2)若AE=CF,能否说明BE=DF?若能,请说明理由;若不能,请画出反例.
(本题8分)如图,张大叔从市场上买回一块矩形铁皮,他将此矩形铁皮的四个角各剪去一个边长为1米的正方形后,剩下的部分刚好能围成一个容积为15米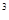 的无盖长方体箱子,且此长方体箱子的底面长比宽多2米,现已知购买这种铁皮每平方米需20元钱,问张大叔购回这张矩形铁皮共花了多少元钱?
的无盖长方体箱子,且此长方体箱子的底面长比宽多2米,现已知购买这种铁皮每平方米需20元钱,问张大叔购回这张矩形铁皮共花了多少元钱?
(本题8分)在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于F,且AF=BD,连接BF.
(1)求证:BD=CD.
(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.
(本题12分)如图,已知 ,
, 是一次函数
是一次函数 的图象和反比例函数
的图象和反比例函数 的图象的两个交点.
的图象的两个交点.
(1)求一次函数、反比例函数的关系式;
(2)求△AOB的面积.
(3)当自变量x满足什么条件时,y1>y2.(直接写出答案)(4)将反比例函数 的图象向右平移n(n>0)个单位,得到的新图象经过点(3,-4),求对应的函数关系式y3.(直接写出答案)
的图象向右平移n(n>0)个单位,得到的新图象经过点(3,-4),求对应的函数关系式y3.(直接写出答案)
(本题6分)矩形纸片ABCD中,AB=5,AD=4.
(1)如图1,四边形MNEF是在矩形纸片ABCD中裁剪出的一个正方形.你能否在该矩形中裁剪出一个面积最大的正方形,最大面积是 ;(不必说明理由)
(2)请用矩形纸片ABCD剪拼成一个面积最大的正方形.要求:在图2的矩形ABCD中画出裁剪线,并在网格中画出用裁剪出的纸片拼成的正方形示意图(使正方形的顶点都在网格的格点上).
(本题12分)如图,ABCD是一张矩形纸片,AD=BC=1,AB=CD=5.在矩形ABCD的边AB上取一点M,在CD上取一点N,将纸片沿MN折叠,使MB与DN交于点K,得到△MNK.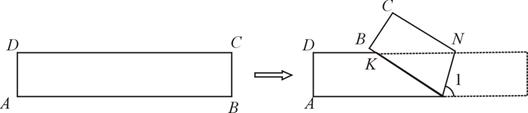
(1)若∠1=70°,求∠MKN的度数.
(2)△MNK的面积能否小于 ?若能,求出此时∠1的度数;若不能,试说明理由.
?若能,求出此时∠1的度数;若不能,试说明理由.
(3)如何折叠能够使△MNK的面积最大?请你利用备用图探究可能出现的情况,求出最大值.
(本题12分)阅读理解:配方法是中学数学的重要方法,用配方法可求最大(小)值。如对于任意正实数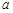 、x,可作变形:x+
、x,可作变形:x+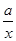 =(
=(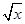 -
-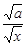 )2+2
)2+2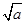 ,因为(
,因为(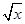 -
-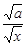 )2≥0,所以x+
)2≥0,所以x+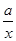 ≥2
≥2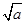 (当x=
(当x=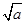 时取等号).
时取等号).
记函数y=x+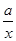 (a>0,x>0),由上述结论可知:当x=
(a>0,x>0),由上述结论可知:当x=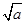 时,该函数有最小值为2
时,该函数有最小值为2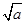 .
.
直接应用: 已知函数y1=x(x>0)与函数y2 = 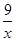 (x>0),则当x= 时,y1+y2取得最小值为 .
(x>0),则当x= 时,y1+y2取得最小值为 .
变形应用: 已知函数y1=x+1(x>-1)与函数y2=(x+1)2+4(x>-1),求 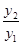 的最小值,并指出取得该最小值时相应的x的值.
的最小值,并指出取得该最小值时相应的x的值.
实际应用:汽车的经济时速是指汽车最省油的行驶速度。某种汽车在每小时70~110公里之间行驶时(含70公里和110公里),每公里耗油(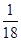 +
+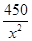 )升。若该汽车以每小时x公里的速度匀速行驶,1小时的耗油量为y升.
)升。若该汽车以每小时x公里的速度匀速行驶,1小时的耗油量为y升.
①求y关于x的函数关系式(写出自变量x的取值范围);
②求该汽车的经济时速及经济时速的百公里耗油量(结果保留小数点后一位).

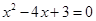 时可配方得 ( )
时可配方得 ( )
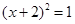


 粤公网安备 44130202000953号
粤公网安备 44130202000953号