浙江省舟山市一学九年级上学期期中考试数学试卷
反比例函数 的图象在( )
的图象在( )
| A.第一、三象限 | B.第二、四象限 |
| C.第一、二象限 | D.第三、四象限 |
已知二次函数的解析式为 ,则该二次函数图象的顶点坐标是( )
,则该二次函数图象的顶点坐标是( )
| A.(-2,1) | B.(2,1) | C.(2,-1) | D.(1,2) |
把二次函数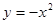 的图象先向右平移1个单位,再向上平移2个单位后得到一个新图象,则新图象所表示的二次函数的解析式是( )
的图象先向右平移1个单位,再向上平移2个单位后得到一个新图象,则新图象所表示的二次函数的解析式是( )
A.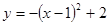 |
B.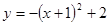 |
C.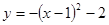 |
D.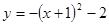 |
下列关于反比例函数的叙述,不正确的是( )
A.反比例函数y= 的图象绕原点旋转180°后,能与原来的图象重合 的图象绕原点旋转180°后,能与原来的图象重合 |
B.反比例函数y= 的图象既不与x轴相交,也不与y轴相交 的图象既不与x轴相交,也不与y轴相交 |
C.反比例函数y= 的图象关于直线 的图象关于直线 成轴对称 成轴对称 |
D.反比例函数y= ,当k>0时,y随x的增大而减少 ,当k>0时,y随x的增大而减少 |
如图,边长为2的菱形ABCD绕点A旋转,当B、C两点恰好落在扇形AEF的弧EF上时,弧BC的长度等于( )
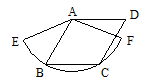
A.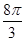 B.
B. C.
C.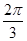 D.
D.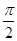
根据下列表格的对应值:

判断方程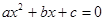 (
(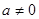 ,
,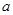 、
、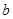 、
、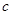 为常数)一个解的范围是( )
为常数)一个解的范围是( )
| A.3<x<3.23 | B.3.23<x<3.24 |
| C.3.24<x<3.25 | D.3.25<x<3.26 |
已知n是正整数,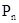 (
(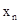 ,
,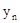 )是反比例函数
)是反比例函数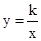 图象上的一列点,其中
图象上的一列点,其中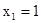 ,
,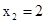 ,…,
,…,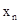 =n; 记
=n; 记 ,
,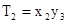 ,…,
,…,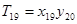 ;若
;若 ,则
,则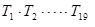 的值是( )
的值是( )
| A.0.1×218 | B.0.1×219 |
| C.0.1×220 | D.0.1×221 |
能确定二次函数y=ax2+bx+c的图象如图所示,则下列结论:①、abc<0;②、a-b+c<0;③、b2-4ac>0;④、b+2a=0;⑤b+2c<0;其中不正确的个数是:( )

| A.1个 | B.2个 | C.3个 | D.4个 |
设抛物线y=-x2+8x-12与X轴的两个交点是A、B,与y轴的交点为C,则△ABC的面积是 .
如图,在正方形纸板上剪下一个扇形和圆,围成一个圆锥模型,设围成的圆锥底面半径为r,母线长为R,则r与R之间的倍数关系是 .


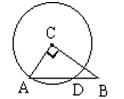
如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,以C为圆心,CA为半径的圆交斜边于D,则BD的长为 cm.
已知反比例函数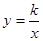 经过点(l,2).
经过点(l,2).
(1)求k的值;
(2)若反比例函数的图象经过点P(a,a-1),求a的值.
如图,已知矩形ABCD中,AB=1cm,BC=2cm,以B为圆心,BC为半径作 圆弧交AD于F,交BA的延长线于E,求扇形BCE被矩形所截剩余部分的面积.
圆弧交AD于F,交BA的延长线于E,求扇形BCE被矩形所截剩余部分的面积.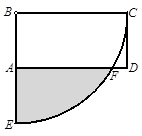
如图,一个二次函数的图象经过点A、C、B三点,点A的坐标为( ),点B的坐标为(
),点B的坐标为(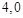 ),点C在y轴的正半轴上,且AB=OC.
),点C在y轴的正半轴上,且AB=OC.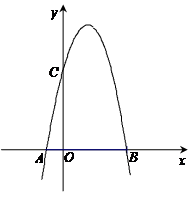
(1)求点C的坐标;
(2)求这个二次函数的解析式,并求出该函数的最大值.
如图,以△ABC的边AB为直径作⊙O,交BC于D点,交AC于E点,BD=DE.
(1)求证:△ABC是等腰三角形
(2)若E是AC的中点,求弧BD的度数.
制作一种产品,需先将材料加热达到60℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(分钟).据了解,设该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图).已知该材料在操作加工前的温度为15℃,加热5分钟后温度达到60℃.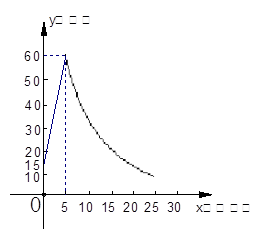
(1)分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;
(2)根据工艺要求,当材料的温度低于20℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?
如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处.
(1)直接写出点E、F的坐标;
(2)在y轴上是否存在点M,使得三角形MFE的周长最小?如果存在,求出周长的最小值;如果不存在,请说明理由.
(3)设顶点为F的抛物线交y轴正半轴于点P,且以点E、F、P为顶点的三角形是等腰三角形,求该抛物线的解析式;若顶点为F的抛物线交y轴负半轴于点P,且以点E、F、P为顶点的三角形是等腰三角形, 请直接写出点P的坐标.
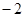 的倒数是( )
的倒数是( )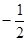
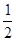
 ,则圆周角
,则圆周角 的度数是( )
的度数是( )




 ,OP=
,OP= ,则点P与⊙O的相对位置是:P在⊙O .
,则点P与⊙O的相对位置是:P在⊙O .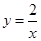 ,当
,当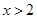 时,y的取值范围是_____.
时,y的取值范围是_____. +〔
+〔 -
- 〕-
〕-

 粤公网安备 44130202000953号
粤公网安备 44130202000953号