(1)如图1,是正方形
边
上的一点,连接
、
,将
绕点
逆时针旋转
,旋转后角的两边分别与射线
交于点
和点
.
①线段和
的数量关系是 ;
②写出线段,
和
之间的数量关系.
(2)当四边形为菱形,
,点
是菱形
边
所在直线上的一点,连接
、
,将
绕点
逆时针旋转
,旋转后角的两边分别与射线
交于点
和点
.
①如图2,点在线段
上时,请探究线段
、
和
之间的数量关系,写出结论并给出证明;
②如图3,点在线段
的延长线上时,
交射线
于点
,若
,
,直接写出线段
的长度.

如图,直线与
轴,
轴分别交于
,
两点,过
,
两点的抛物线
与
轴交于点
.
(1)求抛物线的解析式;
(2)连接,若点
是线段
上的一个动点(不与
,
重合),过点
作
,交
于点
,当
的面积是
时,求点
的坐标;
(3)在(2)的结论下,将绕点
旋转
得△
,试判断点
是否在抛物线上,并说明理由.

如图1是实验室中的一种摆动装置,在地面上,支架
是底边为
的等腰直角三角形,摆动臂
可绕点
旋转,摆动臂
可绕点
旋转,
,
.
(1)在旋转过程中,
①当,
,
三点在同一直线上时,求
的长.
②当,
,
三点为同一直角三角形的顶点时,求
的长.
(2)若摆动臂顺时针旋转
,点
的位置由
外的点
转到其内的点
处,连结
,如图2,此时
,
,求
的长.

如图,在平面直角坐标系中,抛物线与
轴交于点
,
(点
在点
的左侧),交
轴于点
,点
为抛物线的顶点,对称轴与
轴交于点
.
(1)连结,点
是线段
上一动点(点
不与端点
,
重合),过点
作
,交抛物线于点
(点
在对称轴的右侧),过点
作
轴,垂足为
,交
于点
,点
是线段
上一动点,当
取得最大值时,求
的最小值;
(2)在(1)中,当取得最大值,
取得最小值时,把点
向上平移
个单位得到点
,连结
,把
绕点
顺时针旋转一定的角度
,得到△
,其中边
交坐标轴于点
.在旋转过程中,是否存在一点
,使得
?若存在,请直接写出所有满足条件的点
的坐标;若不存在,请说明理由.

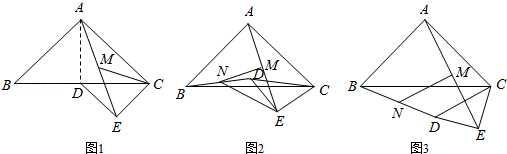
已知 是等腰直角三角形, , , , ,连接 ,点 是 的中点.
(1)如图1,若点 在 边上,连接 ,当 时,求 的长;
(2)如图2,若点 在 的内部,连接 ,点 是 中点,连接 , ,求证: ;
(3)如图3,将图2中的 绕点 逆时针旋转,使 ,连接 ,点 是 中点,连接 ,探索 的值并直接写出结果.
在平面直角坐标系中, 为原点,点 ,点 ,把 绕点 逆时针旋转,得△ ,点 , 旋转后的对应点为 , ,记旋转角为 .
(Ⅰ)如图①,若 ,求 的长;
(Ⅱ)如图②,若 ,求点 的坐标;
(Ⅲ)在(Ⅱ)的条件下,边 上 的一点 旋转后的对应点为 ,当 取得最小值时,求点 的坐标(直接写出结果即可)

在中,
,
.点
是平面内不与点
,
重合的任意一点.连接
,将线段
绕点
逆时针旋转
得到线段
,连接
,
,
.
(1)观察猜想
如图1,当时,
的值是 ,直线
与直线
相交所成的较小角的度数是 .
(2)类比探究
如图2,当时,请写出
的值及直线
与直线
相交所成的较小角的度数,并就图2的情形说明理由.
(3)解决问题
当时,若点
,
分别是
,
的中点,点
在直线
上,请直接写出点
,
,
在同一直线上时
的值.
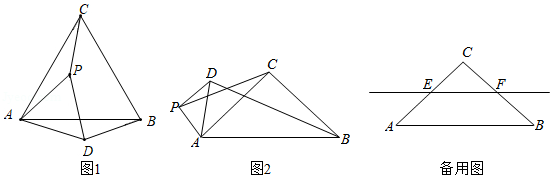
(1)发现:如图1,点 为线段 外一动点,且 , .
填空:当点 位于 时,线段 的长取得最大值,且最大值为 (用含 , 的式子表示)
(2)应用:点 为线段 外一动点,且 , ,如图2所示,分别以 , 为边,作等边三角形 和等边三角形 ,连接 , .
①请找出图中与 相等的线段,并说明理由;
②直接写出线段 长的最大值.
(3)拓展:如图3,在平面直角坐标系中,点
的坐标为
,点
的坐标为
,点
为线段
外一动点,且
,
,
,请直接写出线段
长的最大值及此时点
的坐标. 
问题发现
(1)如图(1),四边形 中,若 , ,则线段 , 的位置关系为 ;
拓展探究
(2)如图(2),在 中,点 为斜边 的中点,分别以 , 为底边,在 外部作等腰三角形 和等腰三角形 ,连接 , ,分别交 , 于点 , ,试猜想四边形 的形状,并说明理由;
解决问题
(3)如图(3),在正方形 中, ,以点 为旋转中心将正方形 旋转 ,得到正方形 ,请直接写出 的长度.

已知,
为射线
上一定点,
,
为射线
上一点,
为线段
上一动点,连接
,满足
为钝角,以点
为中心,将线段
顺时针旋转
,得到线段
,连接
.
(1)依题意补全图1;
(2)求证:;
(3)点关于点
的对称点为
,连接
.写出一个
的值,使得对于任意的点
总有
,并证明.
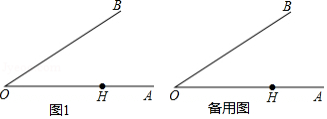
(1)如图,把∠AOB绕着O点按逆时针方向旋转一个角度,得∠A′OB′,指出图中所有相等的角.
(2)如图,BD平分∠ABC,BE分∠ABC分2:5两部分,∠DBE=21°,求∠ABC的度数.
如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.
(年贵州省黔南州)如图,在平面直角坐标系xOy中,抛物线 过点A(0,4)和C(8,0),P(t,0)是x轴正半轴上的一个动点,M是线段AP的中点,将线段MP绕点P顺时针旋转90°得线段PB,过点B作x轴的垂线,过点A作y轴的垂线,两直线交于点D.
过点A(0,4)和C(8,0),P(t,0)是x轴正半轴上的一个动点,M是线段AP的中点,将线段MP绕点P顺时针旋转90°得线段PB,过点B作x轴的垂线,过点A作y轴的垂线,两直线交于点D.
(1)求b、c的值;
(2)当t为何值时,点D落在抛物线上;
(3)是否存在t,使得以A,B,D为顶点的三角形与△AOP相似?若存在,求此时t的值;若不存在,请说明理由.