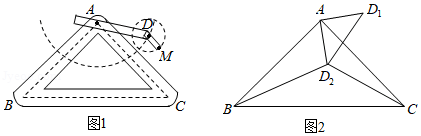
如图1是实验室中的一种摆动装置,在地面上,支架是底边为的等腰直角三角形,摆动臂可绕点旋转,摆动臂可绕点旋转,,.
(1)在旋转过程中,
①当,,三点在同一直线上时,求的长.
②当,,三点为同一直角三角形的顶点时,求的长.
(2)若摆动臂顺时针旋转,点的位置由外的点转到其内的点处,连结,如图2,此时,,求的长.
相关知识点
推荐套卷
如图1是实验室中的一种摆动装置,在地面上,支架是底边为的等腰直角三角形,摆动臂可绕点旋转,摆动臂可绕点旋转,,.
(1)在旋转过程中,
①当,,三点在同一直线上时,求的长.
②当,,三点为同一直角三角形的顶点时,求的长.
(2)若摆动臂顺时针旋转,点的位置由外的点转到其内的点处,连结,如图2,此时,,求的长.
