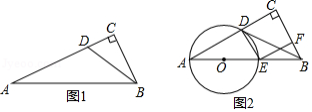
定义:三角形一个内角的平分线和与另一个内角相邻的外角平分线相交所成的锐角称为该三角形第三个内角的遥望角.
(1)如图1, 是 中 的遥望角,若 ,请用含 的代数式表示 .
(2)如图2,四边形 内接于 , ,四边形 的外角平分线 交 于点 ,连结 并延长交 的延长线于点 .求证: 是 中 的遥望角.
(3)如图3,在(2)的条件下,连结 , ,若 是 的直径.
①求 的度数;
②若 , ,求 的面积.

已知四边形 是 的内接四边形, 是 的直径, ,垂足为 .
(1)延长 交 于点 ,延长 , 交于点 ,如图1.求证: ;
(2)过点 作 ,垂足为 , 交 于点 ,且点 和点 都在 的左侧,如图2.若 , , ,求 的大小.

如图,在 中, ,以 为直径的 交 于点 , 是 的中点, 交 于点 .
(1)若 , ,求 的长;
(2)判断直线 与 的位置关系,并说明理由;
(3)求证: .

如图,点 是 直径 延长线上的一点, 在 上, ,
(1)求证: 是 的切线;
(2)若 的半径为2,求 的面积.

如图1, 中, ,点 在 上, ,过 、 两点的圆的圆心 在 上.
(1)利用直尺和圆规在图1中画出 (不写作法,保留作图痕迹,并用黑色水笔把线条描清楚);
(2)判断 所在直线与(1)中所作的 的位置关系,并证明你的结论;
(3)设 交 于点 ,连接 ,过点 作 , 为垂足,若点 是线段 的黄金分割点(即 ,如图2,试说明四边形 是正方形).
(2) , ,
,
;
又 ,
,
;
方法一:在 中, ,
连接 ,设 的半径为 ,则在 中, ,即
解得:
方法二: ,过点 作 于点 ,则
在 中,

本题考查了圆的综合题:圆的切线垂直于过切点的半径;利用勾股定理计算线段的长.
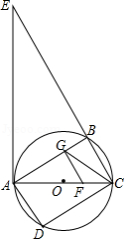
如图,四边形 内接于圆 , , 为直径,过点 作圆 的切线交 的延长线于点 ,过 的三等分点 (靠近点 作 的平行线交 于点 ,连接 .
(1)求证: ;
(2)求证: ;
(3)当 , 时,求 的长.
如图, 为 的直径, 、 是 的切线,切点分别为点 、 ,点 为线段 上的一个动点,连接 , , ,已知 , ,当 的值最小时,则 的值为

A. B. C. D.
如图, 是以 为直径的 的切线, 为切点, 平分 ,弦 交 于点 , .
(1)求证: 是等腰直角三角形;
(2)求证: ;
(3)求 的值.

如图,已知 , , , 与 、 均相切,点 是线段 与抛物线 的交点,则 的值为
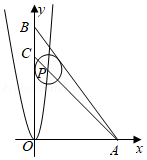
| A. | 4 |
B. |
|
C. |
|
D. | 5 |
如图1, 是 的直径 上的一点,过 作 交 于 、 , 是 上的一点,过 的直线分别与 、 的延长线相交于 、 ,连接 交 于 , .
(1)求证: 是 的切线;
(2)若 , 的半径为4, ,求 的长;
(3)如图2,在(2)的条件下,连接 、 ;在线段 上有一点 ,并且以 、 、 为顶点的三角形与 相似,求 的长度.

如图,以原点 为圆心,3为半径的圆与 轴分别交于 , 两点(点 在点 的右边), 是半径 上一点,过 且垂直于 的直线与 分别交于 , 两点(点 在点 的上方),直线 , 交于点 .若 .
(1)求点 的坐标;
(2)求过点 和点 ,且顶点在直线 上的抛物线的函数表达式.

如图,已知 为 的角平分线, , ,以 为圆心, 为半径的圆分别交 , 于点 , ,连接 并延长交 于点 .
(1)求证: 是 的切线;
(2)求 的值;
(3)求 的值.

如图, 是 的直径,弦 ,垂足为 ,连接 ,过 上一点 作 交 的延长线于点 ,连接 交 于点 ,且 ,连接 .
(1)求证: ;
(2)求证: 是 的切线;
(3)延长 交 的延长线于点 ,若 , ,求 的值.
