(2) , ,
,
;
又 ,
,
;
方法一:在 中, ,
连接 ,设 的半径为 ,则在 中, ,即
解得:
方法二: ,过点 作 于点 ,则
在 中,
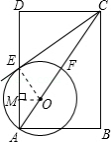
本题考查了圆的综合题:圆的切线垂直于过切点的半径;利用勾股定理计算线段的长.
推荐套卷
(2) , ,
,
;
又 ,
,
;
方法一:在 中, ,
连接 ,设 的半径为 ,则在 中, ,即
解得:
方法二: ,过点 作 于点 ,则
在 中,

本题考查了圆的综合题:圆的切线垂直于过切点的半径;利用勾股定理计算线段的长.