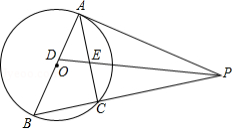
如图, 是以 为直径的半圆 的切线, 为半圆上一点, , , 的延长线相交于点 .
(1)求证: 是半圆 的切线;
(2)连接 ,求证: ;
(3)若 , ,求 的长.
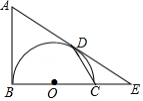
已知:如图,在 中, , 与 相切于点 .求证: .小明同学的证明过程如下框:
证明:连结 , , , 又 , , . |
小明的证法是否正确?若正确,请在框内打“ ”;若错误,请写出你的证明过程.
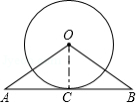
如图,已知一次函数 的图象与反比例函数 的图象交于点 ,且与 轴交于点 ,第一象限内点 在反比例函数 的图象上,且以点 为圆心的圆与 轴, 轴分别相切于点 ,
(1)求 的值;
(2)求一次函数的表达式;
(3)根据图象,当 时,写出 的取值范围.
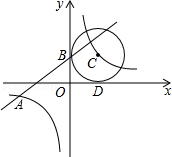
如图, 是 的直径, 为 上一点, 和过点 的切线互相垂直,垂足为 .
(1)求证: ;
(2)若 , ,求 的长.

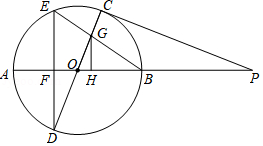
如图,已知 , 是 的直径,过点 作 的切线交 的延长线于点 , 的弦 交 于点 ,且 .
(1)求证: ;
(2)连接 交 于点 ,过点 作 于点 ,若 , ,求 的长.
我们学习过利用尺规作图平分一个任意角,而“利用尺规作图三等分一个任意角”曾是数学史上一大难题,之后被数学家证明是不可能完成的.人们根据实际需要,发明了一种简易操作工具 三分角器.图1是它的示意图,其中 与半圆 的直径 在同一直线上,且 的长度与半圆的半径相等; 与 垂直于点 , 足够长.
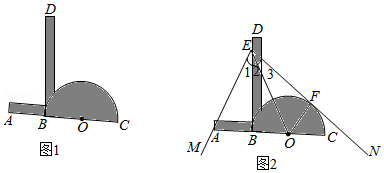
使用方法如图2所示,若要把 三等分,只需适当放置三分角器,使 经过 的顶点 ,点 落在边 上,半圆 与另一边 恰好相切,切点为 ,则 , 就把 三等分了.
为了说明这一方法的正确性,需要对其进行证明.如下给出了不完整的“已知”和“求证”,请补充完整,并写出“证明”过程.
已知:如图2,点 , , , 在同一直线上, ,垂足为点 , .
求证: .
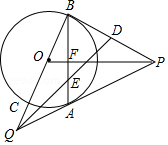
如图, 是 外的一点, 、 是 的两条切线, 、 是切点, 交 于点 ,延长 交 于点 ,交 的延长交于点 ,连接 .
(1)求证: ;
(2)设 为 的中点, 交 于点 ,若 的半径为3, ,求 的值.
如图,在 中, ,以 的中点 为圆心, 为直径的圆交 于 , 是 的中点, 交 的延长线于 .
(1)求证: 是圆 的切线:
(2)若 , ,求 的长.

如图, 是 的直径, 与 相切于点 ,与 的延长线交于点 , 于点 .
(1)求证: ;
(2)若 , ,求 的半径.

如图,在 中,直径
中,直径 垂直于不过圆心
垂直于不过圆心 的弦
的弦 ,垂足为点
,垂足为点 ,连接
,连接 ,点
,点 在
在 上,且
上,且
(1)求证: ;
;
(2)过点 作
作 的切线交
的切线交 的延长线于点
的延长线于点 ,试判断
,试判断 与
与 是否相等,并说明理由;
是否相等,并说明理由;
(3)设 半径为4,点
半径为4,点 为
为 中点,点
中点,点 在
在 上,求线段
上,求线段 的最小值.
的最小值.

如图,已知 为 直径, 是 的切线,连接 交 于点 ,取 的中点 ,连接 交 于点 ,过点 作 于 .
(1)求证: ;
(2)若 , ,求 和 的长.
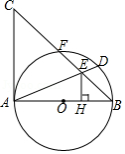
如图, 是 的直径, 为弦, 的平分线交 于点 ,过点 的切线交 的延长线于点 .
求证:(1) ;
(2) .

如图,已知 、 为 的两条直径, 为切线,过 上一点 作 于 ,连接 并延长交 于点 ,连接 .
(1)求证: .
(2)设 为点 关于 对称点,连接 、 ,如果 , 的半径为3,求 的值.

如图,以 为直径的 外接于 ,过 点的切线 与 的延长线交于点 , 的平分线分别交 , 于点 , ,其中 , 的长是一元二次方程 的两个实数根.
(1)求证: ;
(2)在线段 上是否存在一点 ,使得四边形 是菱形?若存在,请给予证明,并求其面积;若不存在,说明理由.