初中数学圆内接四边形的性质解答题

如图，在矩形ABCD中，AB=6cm，BC=12cm，点P从点A沿边AB向点B以1cm/s的速度移动；同时，点Q从点B沿边BC向点C以2cm/s的速度移动，有一点到终点运动即停止．问：

（1）几秒钟后△PBQ的面积等于8cm²？
（2）几秒钟后PQ⊥DQ？
（3）是否存在这样的时刻，使S_△PDQ=8cm²，试说明理由．

小明家的房前有一块矩形的空地，空地上有三棵树A、B、C，小明想建一个圆形花坛，使三棵树都在花坛的边上．
（1）请你帮小明把花坛的位置画出来（尺规作图，不写作法，保留作图痕迹）；
（2）若△ABC中AB=8米，AC=6米，∠BAC=90°，试求小明家圆形花坛的面积．

如图1，正方形ABCD中，E、F分别在AD、DG上，EF的延长线交BC的延长线于G点，且∠AEB=∠BEG；

（1）求证：∠ABE=∠BGE；
（2）如图2，若AB=5，AE=2，求S_△BEG；
（3）如图3，若E、F两点分别在AD、DC上运动，其它条件不变，试问：线段AE、EF、FC三者之间是否存在确定的数量关系？若存在，请写出它们之间的数量关系，并证明；若不存在，请说明理由．

如图，在△ABC中，∠ACB=90°，CD是AB边上的高，∠BAC的平分线AE交C于F，EG⊥AB于G，请判断四边形GECF的形状，并证明你的结论．

如图，要用一块长4米、宽2米的长方形木板，拼接出一块长5米、宽1．5米的长方形木板，为了保证牢固，要求接缝条数尽可能地少．你能用自己学过的图形全等的有关知识设计一个拼接方案吗？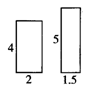

在等腰直角三角形ABC中，∠BAC=90°，AB=AC，直线MN过点A且MN∥BC，过点B为一锐角顶点作Rt△BDE，∠BDE=90°，且点D在直线MN上（不与点A重合），如图1，DE与AC交于点P，易证：BD=DP．（无需写证明过程）

（1）在图2中，DE与CA延长线交于点P，BD=DP是否成立？如果成立，请给予证明；如果不成立，请说明理由；
（2）在图3中，DE与AC延长线交于点P，BD与DP是否相等？请直接写出你的结论，无需证明．

如图，已知Rt△ABC中，∠ABC=90°，先把△ABC绕点B顺时针旋转90°至△DBE后，再把△ABC沿射线平移至△FEG，DE、FG相交于点H．

（1）判断线段DE、FG的位置关系，并说明理由；
（2）连结CG，求证：四边形CBEG是正方形．

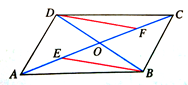
如图，分别延长平行四边形ABCD的边CD、AB到E、F，使DE=BF=CD，连接EF，分别交AD，BC于G，H，连接CG，AH

（1）求证：四边形AGCH为平行四边形；
（2）求△DEG和△CGH的面积比．

已知，矩形中，，，的垂直平分线分别交、 于点、，垂足为.

（1）如图26－1，连接、.求证四边形为菱形，并求的长；
（2）如图26－2，动点、分别从、两点同时出发,沿和各边匀速运动一周.即点自→→→停止，点自→→→停止.在运动过程中.
①已知点的速度为每秒10，点的速度为每秒6，运动时间为秒，当、、、 四点为顶点的四边形是平行四边形时，求的值.
②若点、的运动路程分别为、 （单位:，），已知、、、四点为顶点的四边形是平行四边形，求与满足的函数关系式.

如图，已知四边形ABDE是平行四边形，C为边BD延长线上一点，连结AC、CE，使AB=AC．

（1）求证：△BAD≌△AEC；
（2）若∠B=30°，∠ADC=45°，BD=10，求平行四边形ABDE的面积．

如图1，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE．求证：CE=CF．
（2）如图2，在正方形ABCD中，E是AB上一点，G是AD上一点，如果∠GCE=45°，请你利用（1）的结论证明：GE=BE+GD．

如图，平行四边形ABCD的对角线AC，BD交于点0，E，F在AC上，G，H在BD上，且AF=CE，BH=DG．

求证：FG∥HE．

已知：如图，在△ABC中，AB=AC，AD⊥BC垂足为D，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为E，DE交AC于点F.

（1）求证：四边形ADCE是矩形；
（2）猜想线段DF和AB有何数量关系，并说明理由；
（3）直接写出当△ABC满足什么条件时，四边形ADCE是正方形？

如图，在□ABCD中，AB=2  BC=4，点E、F分别是BC、AD的中点．

（1）求证：△ABE≌△CDF；
（2）当四边形AECF为菱形时，求出该菱形的面积．

如图，□ABCD的对角线AC，BD相交于点O，E，F分别是OA，OC的中点.
求证：BE=DF.