如图，已知△ABC的中线BD、CE相交于点O、M、N分别为OB、OC的中点．
（1）求证：MD和NE互相平分；
（2）若BD⊥AC，EM=2
，OD+CD=7，求△OCB的面积．
如图，▱ABCD中，点E、F分别在边AD、BC上，且AE=CF，连接BE、DF．求证：BE∥DF．
将矩形ABCD折叠使A，C重合，折痕交BC于E，交AD于F，
（1）求证：四边形AECF为菱形；
（2）若AB=4，BC=8，求菱形的边长；
（3）在（2）的条件下折痕EF的长．
如图，已知平行四边形ABCD，延长BC至E，使CE=BC，连接AC，DE，求证：AC=DE．
已知：如图，在▱ABCD中，O为对角线BD的中点，过点O的直线EF分别交AD，BC于E，F两点，连结BE，DF．
（1）求证：△DOE≌△BOF；
（2）当∠DOE等于多少度时，四边形BFDE为菱形？请说明理由．
如图，在直角梯形ABCD中，AD∥BC，∠D=∠C=90°，点E在DC上，且AE，BE分别平分∠BAD和∠ABC．
（1）求证：点E为CD中点；
（2）当AD=2，BC=3时，求AB的长．
如图：已知在△ABC中，AB=AC，D为BC边的中点，过点D作DE⊥AB，DF⊥AC，垂足分别为E，F．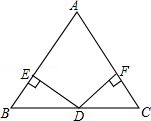
（1）求证：△BED≌△CFD；
（2）若∠A=90°，求证：四边形DFAE是正方形．
如图，已知，在Rt△ABC中，∠BAC=90°．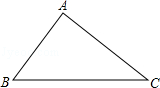
实践与操作：
（1）①利用尺规按下列要求作图，并在图中标明相应的字母（保留作图痕迹，不写作法）：作线段AC的垂直平分线MN，垂足为O；
②连接BO，并延长BO到点D，使得OD=BO，连接AD、CD；
③分别在OA、OC的延长线上取点E、F，使AE=CF，连接BF、FD、DE、EB．
推理与运用：
（2）①求证：四边形BFDE是平行四边形；
②若AB=4，AC=6，求当AE的长为多少时，四边形BFDE是矩形．
如图，在平四边形ABCD中，对角线AC与BD相交于点O，P为线段BC上一点（除端点外），连接PO并延长交AD于点Q，延长BC到点E，使CE=BC，连接DE．
（1）求证：BP=DQ；
（2）已知AB=5，AC=6，若CD=
BE，求△BDE的周长．
长方形纸片ABCD中，AD=4cm，AB=10cm，按如图方式折叠，使点B与点D重合，折痕为EF，求DE的长．
如图，在△ABC中，点D是BC的中点，点F是AD的中点，过点D作DE∥AC，交CF的延长线于点E，连接BE，AE．
（1）求证：四边形ACDE是平行四边形；
（2）若AB=AC，试判断四边形ADBE的形状，并证明你的结论．
如图，矩形ABCD的对角线相交于点O，DE∥AC，CE∥BD．
求证：四边形OCED是菱形．
将平行四边形纸片ABCD按如图方式折叠，使点C与A重合，点D落到D′ 处，折痕为EF．
（1）求证：△ABE≌△AD′F；
（2）连接CF，判断四边形AECF是什么特殊四边形？证明你的结论．
如图，四边形ABCD是平行四边形，AC、BD交于点O，且∠1=∠2，
（1）求证：四边形ABCD是矩形
（2）若∠AOB=60°，AB=8，求BC的长.
如图，在正方形ABCD中，E为ED边上的一点，CE=CF,∠FDC=30°，求∠BEF的度数.
粤公网安备 44130202000953号