初中数学圆内接四边形的性质解答题

如图，在□ABCD中，E、F分别为AC、CA延长线上的点，且CE=AF，请你探讨线段BF与DE位置及大小关系如何．

一个多边形的内角和是它的外角和的4倍，求这个多边形的边数．

如图1，△ABC中，∠ACB=90°，E是AB的中点， ED平分∠BEC交BC于点D，F在DE延长线上且AF=AE．

（1）求证：四边形ACEF是平行四边形；
（2）如图2若四边形ACEF是菱形，连接FC，BF，FC与AB交于点H，连接DH，在不添加任何辅助线的情况下，请直接写出图2中的所有等边三角形

【提出问题】如图1，小东将一张AD为12，宽AB为4的长方形纸片按如下方式进行折叠：在纸片的一边BC上分别取点P、Q，使得BP=CQ，连结AP、DQ，将△ABP、△DCQ分别沿AP、DQ折叠得△APM，△DQN，连结MN．小东发现线段MN的位置和长度随着点P、Q的位置发生改变．

【规律探索】
（1）请在图1中过点M，N分别画ME⊥BC于点E，NF⊥BC于点F．
求证：①ME=NF；②MN∥BC．
【解决问题】
（2）如图1，若BP=3，求线段MN的长；
（3）如图2，当点P与点Q重合时，求MN的长．

已知：如图，在△ABC中，D是BC边上的一点，E是AD的中点，过点A作BC的平行线交与BE的延长线于点F，且AF=DC，连接CF．

（1）求证：D是BC的中点；
（2）当AB与AC有何数量关系时，四边形ADCF为矩形，请说明理由．

如图，梯形ABCD中，AD∥BC，点M是BC的中点，且MA=MD．求证：四边形ABCD是等腰梯形．

如图，在△ABC中，D、E分别是AB、AC的中点，过点E作EF∥AB，交BC于点F．

（1）求证：四边形DBFE是平行四边形；
（2）当△ABC满足什么条件时，四边形DBFE是菱形？为什么？

如图，已知△ABC是等腰三角形，顶角∠BAC=α（α＜60°），D是BC边上的一点，连接AD，线段AD绕点A顺时针旋转α到AE，过点E作BC的平行线，交AB于点F，连接DE，BE，DF．

（1）求证：BE=CD；
（2）若AD⊥BC，试判断四边形BDFE的形状，并给出证明．

如图，梯形ABCD中，AD∥BC，点M是BC的中点，且MA=MD．求证：四边形ABCD是等腰梯形．

如图，在▱ABCD中，点O是对角线AC的中点，过点O的直线MN分别交AB、CD于点M、N，连结AN，CM．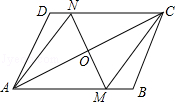

（1）求证：四边形AMCN是平行四边形：
（2）试添加一个条件，使四边形AMCN是菱形，（写出你所添加的条件，不要求证明）

如图，已知：梯形ABCD中，AD∥BC，E为AC的中点，连接DE并延长交BC于点F，连接AF．

（1）求证：AD=CF；
（2）在原有条件不变的情况下，请你再添加一个条件（不再增添辅助线），使四边形AFCD成为菱形，并说明理由．

如图，已知梯形ABCD中，AD∥BC，AC，BD交于O，过O作AD的平行线交AB于M，交CD于N．若AD=3cm，BC=5cm，求ON．

已知：如图，□ABCD的对角线AC的垂直平分线与边AD、BC分别交于E、F．求证：四边形AFCE是菱形．

如图，在平行四边形ABCD中，E、F分别在AD、BC边上，且AE=CF．

求证：（1）△ABE≌△CDF；
（2）四边形BFDE是平行四边形．

已知：如图，在矩形ABCD中，M，N分别是边AD，BC的中点，E，F分别是线段BM，CM的中点．
（1）求证：△ABM≌△DCM；
（2）判断四边形MENF是什么特殊四边形，并证明你的结论；
（3）当AD：AB=            时，四边形MENF是正方形（只写结论，不需证明）．