如图，已知△ABC是等腰三角形，顶角∠BAC=α（α＜60°），D是BC边上的一点，连接AD，线段AD绕点A顺时针旋转α到AE，过点E作BC的平行线，交AB于点F，连接DE，BE，DF．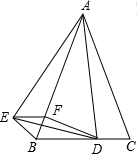
（1）求证：BE=CD；
（2）若AD⊥BC，试判断四边形BDFE的形状，并给出证明．
推荐套卷
如图，已知△ABC是等腰三角形，顶角∠BAC=α（α＜60°），D是BC边上的一点，连接AD，线段AD绕点A顺时针旋转α到AE，过点E作BC的平行线，交AB于点F，连接DE，BE，DF．
（1）求证：BE=CD；
（2）若AD⊥BC，试判断四边形BDFE的形状，并给出证明．
粤公网安备 44130202000953号