初中数学圆内接四边形的性质解答题

如图1是一个长为，宽为的长方形，沿图中虚线剪开，可分成四块小长方形．
（1）求出图1的长方形面积；
（2）将四块小长方形拼成一个图2的正方形，利用阴影部分面积的不同表示方法，直接写出代数式、、之间的等量关系；
（3）把四块小长方形不重叠地放在一个长方形的内部（如图3），未被覆盖的部分用阴影表示．求两块阴影部分的周长和（用含、的代数式表示）．

如图，把长方形纸片ABCD沿EF折叠后，使得点D与点B重合，点C落在点C′的位置上．

（1）若∠1=55°，求∠2，∠3的度数；
（2）若AB=8，AD=16，求AE的长度．

如图，△ABC是一块锐角三角形余料，其中BC=12cm，高AD=8cm，现在要把它裁成一块正方形材料备用，使正方形的一边QM在BC上，其余两个顶点P，N分别在AB，AC上，问这块正方形材料的边长是多少？

如图，□ABCD中，E是CD的延长线上一点，BE与AD交于点F，。

（1）求证：△ABF∽△CEB;
（2）若△DEF的面积为2，求□ABCD的面积。

已知：ABCD的两边AB，AD的长是关于x的方程的两个实数根．
（1）当m为何值时，四边形ABCD是菱形？求出这时菱形的边长；
（2）若AB的长为2，那么ABCD的周长是多少？

阅读：如图（1），点P（x，y）在平面直角坐标系中，过点P作PA⊥x轴，垂足为A，将点P绕垂足A顺时针旋转角得到对应点，我们称点P到点的运动为倾斜运动．例如：点倾斜30°运动后的对应点为．图形E在平面直角坐标系中，图形E上的所有点都作倾斜运动后得到图形，这样的运动称为图形E的倾斜运动．
理解：（1）点倾斜60°运动后的对应点的坐标为          ；
（2）如图（2），平行于x轴的线段MN倾斜运动后得到对应线段，与MN平行且相等吗？说明理由．
应用：（1）如图（3），正方形AOBC倾斜运动后，其各边中点E，F，G，H的对应点，，，构成的四边形是什么特殊四边形：          ；
（2）如图（4），已知点A（0，4）， B（2，0），C（3，2），将△ABC倾斜运动后能不能得到， 且为直角？其中点，，为点A，B，C的对应点．若能，请写出的值，若不能，请说明理由．参考公式： ．

如图,在平行四边形ABCD中,∠ABD=30°，AB=4，BD=，将△BCD沿方向平移，得到△EFG．

（1）连结AE、DF，求证：四边形AEFD为平行四边形．
（2）若□AEFD为矩形，求△BCD平移的距离BE．

（本小题满分6分）如图，已知点A、B、C、D在一条直线上，BF、CE相交于O，AE=DF，∠E=∠F,OB=OC．

（1）求证：△ACE≌△DBF；
（2）如果把△DBF沿AD折翻折使点F落在点G，连接BE和CG，求证：四边形BGCE是平行四边形．

如图是一种儿童的游乐设施—儿童荡板．小明想验证这个荡板上方的四边形是否是平行四边形，现在手头只有一根足够长的绳子，请你帮助他设计一个验证方案，并说明理由．

如图，在△ABC中，AB=AC，∠DAC是△ABC的一个外角．实践与操作：
根据要求尺规作图，并在图中标明相应字母（保留作图痕迹，不写作法）．

（1）作∠DAC的平分线AM；
（2）作线段AC的垂直平分线，与AM交于点F，与BC边交于点E，连接AE、CF．判断四边形AECF的形状并加以证明．

探索证明如图，四边形ABCD中，对角线相交于点O，E、F、G、H分别是AD，BD， BC，AC的中点．

（1）求证：四边形EFGH是平行四边形；
（2）当四边形ABCD满足一个什么条件时，四边形EFGH是菱形？并证明你的结论．
（3）当AB和CD满足什么条件时，四边形EFGH是正方形．（直接写出结论，不必写证明过程）

如图正方形ABCD边长为1，G为CD边上的一个动点（点G与C、D不重合），以CG为一边向正方形ABCD外作正方形GCEF，连接DE交BG的延长线于点H．

（1）求证：BH⊥DE
（2）当BH垂直平分DE时，求CG的长度？请说明理由．（提示：要有辅助线哟？）

（本小题满分6分）如上图，在△ABC和△EDC中，AC＝CE＝CB＝CD，∠ACB＝∠ECD＝90°，AB与CE交于F，ED与AB、BC分别交于M、H．
（1）求证:CF＝CH；
（2）如下图，△ABC不动，将△EDC绕点C旋转到∠BCE=45°时，试判断四边形ACDM是什么四边形？并证明你的结论．

问题探究：
（1）请在图①中作出两条直线，使它们将圆面四等分；
（2）如图②，M是正方形ABCD内一定点，请在图②中作出两条直线（要求其中一条直线必须过点M）使它们将正方形ABCD的面积四等分，并说明理由．
问题解决：
（3）如图③，在四边形ABCD中，AB∥CD，AB+CD=BC，点P是AD的中点，如果AB=a，CD=b，且b＞a，那么在边BC上是否存在一点Q，使PQ所在直线将四边形ABCD的面积分成相等的两部分？如若存在，求出BQ的长；若不存在，说明理由．

如图，在平行四边形ABCD中，AE是BC边上的高，将△ABE沿BC方向平移，使点E与点C重合，得△GFC．

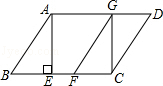
（1）求证：BE=DG；
（2）若∠B=60°，当BC=  AB时，四边形ABFG是菱形；
（3）若∠B=60°，当BC=        AB时，四边形AECG是正方形．