初中数学圆内接四边形的性质解答题

如图，在□ABCD中，F是AD的中点，延长BC到点E，使CE=BC，连结DE，CF。

（1）求证：四边形CEDF是平行四边形；
（2）若AB=4，AD=6，∠B=60°，求DE的长。

如图，四边形ABCD是正方形，BE⊥BF， BE=BF，EF与BC交于点G．

（1）求证：AE=CF；
（2）若∠ABE=55°，求∠EGC的大小．

如图，正方形ABCD中，点E，F分别在边AB，BC上，AF=DE，AF和DE相交于点G，

（1）观察图形，写出图中所有与∠AED相等的角．
（2）选择图中与∠AED相等的任意一个角，并加以证明．

有这样的一个定理：夹在两条平行线间的平行线段相等．下面经历探索与应用的过程．
探索：
已知：如图1，AD∥BC，AB∥CD．求证：AB=CD．
应用此定理进行证明求解．
应用一、已知：如图2，AD∥BC，AD＜BC，AB=CD．求证：∠B=∠C；

应用二、已知：如图3，AD∥BC，AC⊥BD，AC=4，BD=3．求：AD与BC两条线段的和．

如图，长方形纸片中，AB=10，将纸片折叠，使顶点落在边上的点处，折痕的一端点在边上．

（1）如图（1），当折痕的另一端在边上且AE=5时，求AF的长
（2）如图（2），当折痕的另一端在边上且BG=13时，求AF的长．

用四块长为acm、宽为bcm的矩形材料（如图1）拼成一个大矩形（如图2）或大正方形（如图3），中间分别空出一个小矩形A和一个小正方形B．
（1）求（如图1）矩形材料的面积；（用含a，b的代数式表示）
（2）通过计算说明A、B的面积哪一个比较大；
（3）根据（如图4），利用面积的不同表示方法写出一个代数恒等式．

（本小题满分8分）如图，点P是正方形ABCD内一点，点P到点A，B和D的距离分别为1，，．△ADP沿点A旋转至△ABP’，连结PP’，并延长AP与BC相交于点Q．

（1）求证：△APP’是等腰直角三角形；
（2）求∠BPQ的大小；
（3）求CQ的长．

（14）将两块全等的含30°角的三角尺如图1摆放在一起，设较短直角边长为3．
（1）四边形ABCD是平行四边形吗？说出你的结论和理由。
（2）如图2，将Rt△BCD沿射线BD方向平移到Rt△B1C1D1的位置，四边形ABC1D1是平行四边形吗？说出你的结论和理由。
（3）在Rt△BCD沿射线BD方向平移的过程中，当点B的移动距离为多少时四边形ABC1D1为矩形？当点B的移动距离为多少 时，四边形ABC1D1为菱形？

如图，矩形ABCD中，点P是线段AD上一动点，O为BD的中点，PO的延长线交BC于Q。

（1）求证：OP=OQ；
（2）若AD=8厘米，AB=6厘米，P从点A出发，以1厘米/秒的速度向D运动（不与D重合）。设点P运动时间为t秒，请用t表示PD的长；并求t为何值时，四边形PBQD是菱形。

如图在ABCD中，E，F分别为边AB，CD的中点，连接DE、BF、BD．

（1）求证：．
（2）若AD⊥BD，则四边形BFDE是什么特殊四边形？请证明你的结论．

如图，已知A、B、C、D为矩形的四个顶点，AB=16㎝，AD=6㎝，动点P、Q分别从点A、C同时出发，点P以3㎝/s的速度向点B移动，一直到点B为止，点Q以2㎝/s的速度向点D移动．问


（1）P、Q两点从出发开始几秒时，点P点Q间的距离是10厘米．
（2）P、Q两点间距离何时最小。

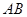（本小题满分14分）如图，在菱形 中， ， 相交于点 ， 为 的中点， ．

（1）求 的度数；
（2）如果 ，求 的长．

如图所示，求∠A+∠B+∠C+∠D+∠E+∠F的度数．

（本题9分）如图，正方形ABCD（四条边相等，四个角是直角）的边长为7cm，点M在边DC上，且CM＝2cm，过点M作 ME⊥DC，交BD于点E．，动点P从点D出发沿DC边向M点运动，速度为每秒2 cm，当动点P到达M点时，运动停止．连接EP，EC．在此过程中，设P点运动时间为t秒．

（1）EM =      cm，
PC =      cm（用含t的代数式表示），
当t =      秒时，△EPC的面积为15？
（2）将△EPC沿CP翻折后，点E的对应点为F点，若PF∥EC，则△EPC为      三角形，请说明理由并求此时t为何值．
（3）是否存在某一时刻，使得P点到A点、E点的距离之和最短？如果存在，直接写出PA+PE的最小值，如果不存在，请说明理由．

如图，四边形ABCD为菱形，M为BC上一点，连接AM，交对角线BD于点G，并且∠ABM＝2∠BAM．

（1）求证：AG＝BG；
（2）若点M为BC的中点，同时S_△BMG＝1，求△ADG的面积．