初中数学圆内接四边形的性质解答题

如图，O是正六边形ABCDEF的中心，连接BD、DF、FB，

（1）设△BDF的面积为S₁，正六边形ABCDEF的面积为S₂ ，则S₁与S₂的数量关系是         ；
（2）△ABF通过旋转可与△CDB重合，请指出旋转中心和最小旋转角的度数．

如图，在△ABC中，AD平分∠BAC，按如下步骤作图：
第一步，分别以点A、D为圆心，以大于AD的长为半径在AD两侧作弧，交于两点M、N；
第二步，连接MN分别交AB、AC于点E、F；
第三步，连接DE、DF．

（1）求证：四边形AEDF是菱形；
（2）若BD=6，AF=4，CD=3，求BE的长．

如图，在△ABC中，AB=AC，D为边BC上一点，以AB，BD为邻边作▱ABDE，连接AD，EC．

（1）求证：△ADC≌△ECD；
（2）若BD=CD，求证：四边形ADCE是矩形

如图，在△ABC中，D是BC边上的一点，E是AD的中点，过A点作BC的平行线交CE的延长线于点F，且AF=BD，连接BF．

（1）线段BD与CD有什么数量关系，并说明理由；
（2）当△ABC满足什么条件时，四边形AFBD是矩形？并说明理由．

如图，菱形ABCD的周长为40cm，它的一条对角线BD长10cm．

（1）求菱形的每一个内角的度数．
（2）求菱形另一条对角线AC的长．

如图，△ABC中，∠A=80°，BE，CF交于点O，∠ACF＝30°，∠ABE＝20°，求∠BOC的度数．

一个多边形的内角和是它的外角和的5倍，求这个多边形的边数．

如图，矩形ABCD中，AB=8，BC=6，P为AD上一点，将△ABP沿BP翻折至△EBP，PE与CD相交于点O，且OE=OD．

（1）求证：OP=OF；
（2）求AP的长．

如图，在完全重合放置的两张长方形纸片ABCD中，AB=4，BC=8，将上面的纸片折叠，使点C与点A重合，折痕为EF，点D的对应点为点G，连接DG，求图中阴影部分的面积．

如图，折叠矩形的一边AD，使点D落在BC边的点F处，AB=8cm，BC=10cm，EC=      cm．

如图：已知在△ABC中，AB=AC，D为BC边的中点，过点D作DE⊥AB，DF⊥AC，，垂足分别为E，F．

（1）求证：△BED≌△CFD；
（2）若∠A=90°，求证：四边形DFAE是正方形．

如图，折叠矩形ABCD的一边AD使点D落在BC边上的E处，已知折痕AF＝10cm，且tan∠FEC＝．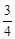

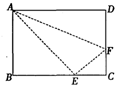
（1）求矩形ABCD的面积；
（2）利用尺规作图求作与四边形AEFD各边都相切的⊙O的圆心O（只须保留作图痕迹），并求出⊙O的半径．

如图，△ABC中，∠ACB=90°，D、E分别是BC、BA的中点，连接DE，F在DE延长线上，且AF=AE．

（1）求证：四边形ACEF是平行四边形；
（2）若四边形ACEF是菱形，求∠B的度数．

在Rt△ABC中，∠BAC=90°，D是BC的中点，E是AD的中点，过点A作AF∥BC交BE的延长线于点F．

（1）求证：△AEF≌△DEB；
（2）证明四边形ADCF是菱形；
（3）若AC=4，AB=5，求菱形ADCF的面积．

已知正方形ABCD中，对角线AC、BD相交于O．
①如图1，若E是AC上的点，过A 作AG⊥BE于G，AG、BD交于F，求证：OE=OF
②如图2，若点E在AC的延长线上，AG⊥EB交EB的延长线于G，AG延长DB延长线于点F，其它条件不变，OE=OF还成立吗？