山东省济南市长清区八年级上学期期中考试数学试卷
在平面直角坐标系中,点(2,﹣4)在( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
下列实数 ,0,π,
,0,π, ,
, ,
, 中是无理数的有( )
中是无理数的有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
以下列各组数为三角形的边长,能构成直角三角形的是( )
| A.1,2,3 | B.5,6,9 | C.5,12,13 | D.8,10,13 |
某木工厂有22人,一个工人每天可加工3张桌子或10只椅子,1张桌子与4只椅子配套,现要求工人每天做的桌子和椅子完整配套而没有剩余,若设安排x个工人加工桌子,y个工人加工椅子,则列出正确的二元一次方程组为( )
A.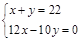 |
B. |
C.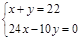 |
D.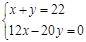 |
点(2,6)关于x轴对称点坐标为( )
| A.(2,﹣6) | B.(﹣2,﹣6) | C.(﹣2,6) | D.(6,2) |
如图,一圆柱高8 cm,底面半径为 cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是( )
cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是( )

| A.6 cm | B.8 cm | C.10 cm | D.12 cm |
一次函数y=kx+b(k≠0)的图象如图所示,则k,b的取值范围是( )

| A.k>0,b>0 | B.k>0,b<0 |
| C.k<0,b>0 | D.k<0,b<0 |
下列各点,在一次函数y=2x+6的图象上的是( )
| A.(﹣5,4) | B.(﹣3.5,1) | C.(4,20) | D.(﹣3,0) |
如图,一次函数y=k1x+b1的图象l1与y=k2x+b2的图象l2相交于点P,则方程组 的解是( )
的解是( )
A. |
B. |
C. |
D. |
如图,在△ABC中,∠ACB=90°,AC=40,BC=9,点M,N在AB上,且AM=AC,BN=BC, 则MN的长为( )

| A.6 | B.7 | C.8 | D.9 |
如图,在直角坐标系中,△AOB是等边三角形,若B点的坐标是(2,0),则A点的坐标是( )

| A.(2,1) | B.(1,2) | C.( ,1 ) ,1 ) |
D.(1, ) ) |
如图,在平面直角坐标系中,已知点A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2),动点P从点A出发,以每秒2个单位的速度按逆时针方向沿四边形ABCD的边做环绕运动;另一动点Q从点C出发,以每秒3个单位的速度按顺时针方向沿四边形CBAD的边做环绕运动,则第2014次相遇点的坐标是( )

| A.(﹣1,﹣1) | B.(﹣1,1) | C.(﹣2,2) | D.(1,2) |
已知一次函数的图象与直线y=﹣x+1平行,且过点(8,2),那么此一次函数的解析式为 .
如图所示是一块长,宽,高分别是6cm,5cm和3cm的长方体木块,一只蚂蚁要从长方体木块的顶点A处,沿着长方体的表面到长方体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长度为 cm

已知P1(1,y1),P2(2,y2)是一次函数y= x-1的图象上的两点,则y1 y2.(填“>”“<”或“=”)
x-1的图象上的两点,则y1 y2.(填“>”“<”或“=”)
如图,折叠矩形的一边AD,使点D落在BC边的点F处,AB=8cm,BC=10cm,EC= cm.

(1)求直线y=2x﹣6与坐标轴的交点坐标.
(2)“中华人民共和国道路交通管理条例”规定:小汽车在城市街道上的行驶速度不得超过70千米 /时.一辆“小汽车”在一条城市街路上直道行驶,某一时刻刚好行驶到路对面“车速检测仪A”正前方50米C处,过了6秒后,测得“小汽车”位置B与“车速检测仪A”之间的距离为130米,这辆“小汽车”超速了吗?请说明理由.
如图,在平面直角坐标系中,
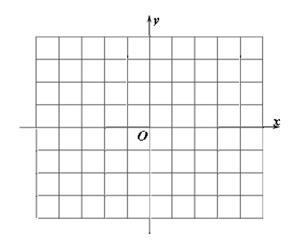
(1)描出A(- 4,3)B(-1,0)C(-2,3)三点.
(2)△ABC的面积是
(3)作出△ABC关于y轴的对称图形.
2014年世界杯足球赛在巴西举行,小李在网上预订了小组赛和淘汰赛两个阶段的球票共10张,总价为5800元.其中小组赛球票每张550元,淘汰赛球票每张700元,问小李预定了小组赛和淘汰赛的球票各多少张?
如图,在平面直角坐标系内,点A的坐标为(0,12),经过原点的直线l,与经过点A的直线12相交于点B,点B的坐标为(9,3).
(1)求直线l1,l2的表达式;
(2)点C为直线l1上一动点,作CD∥y轴交直线l2于点D,若CD=8,求点C的坐标.
某城市居民用水实行阶梯收费,每户每月用水量如果未超过20吨,按每吨1.9元收费.如果超过20吨,未超过的部分按每吨1.9元收费,超过的部分按每吨2.8元收费.设某户每月用水量为x吨,应收水费为y元.
(1)分别写出每月用水量未超过20吨和超过20吨,y与x间的函数关系式;
(2)若该城市某户5月份水费平均为每吨2.2元,求该户5月份用水多少吨?
已知A、B两市相距200千米,甲车从A市前往B市运送物资,行驶2小时在M地汽车出现故障不能行驶,立即通知技术人员乘乙车从A市赶去维修(通知时间忽略不计),乙车到达M地后用24分钟修好甲车后以原速度原路返回,同时甲车以原速1.5倍的速度前往B市,如图是两车距A市的路程y(千米)与甲车的行驶时间x(小时)之间的函数图象,结合图象回答下列问题:

(1)甲车提速后的速度是 千米/小时,点C的坐标是 ,
(2)求乙车返回时y与x之间的函数关系式并写出自变量x的取值范围;
(3)乙车返回A市多长时间后甲车到达B市.
 =( )
=( )



 的解为( )
的解为( )



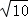 )2+
)2+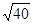 .
. 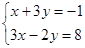
 粤公网安备 44130202000953号
粤公网安备 44130202000953号