广东省深圳市南山二外八年级上学期期中考试数学试卷
在给出的一组数0,π, ,3.14,,
,3.14,,
 中,无理数有( )
中,无理数有( )
| A.1个 | B.2个 | C.3个 | D.5个 |
点P(4,-3)关于y轴的对称点所在的象限是( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
对于一次函数y=x+6,下列结论错误的是( )
| A.函数值随自变量增大而增大 |
| B.函数图象与x轴正方向成45°角 |
| C.函数图象不经过第四象限 |
| D.函数图象与x轴交点坐标是(0,6) |
下列各组数中,以a、b、c为边长的三角形不是直角三角形的是( )
| A.a=1.5,b=2,c="3" | B.a=7,b=24,c=25 |
| C.a=6,b=10,c="8" | D.a=5,b=12,c=13 |
若单项式2x2ya+b与- xa-by4是同类项,则a,b的值分别为( )
xa-by4是同类项,则a,b的值分别为( )
| A.a=3,b="1" | B.a=-3,b="1" | C.a=3,b="-1" | D.a=-3,b=-1 |
直线y=2x+2沿y轴向下平移6个单位后与x轴的交点坐标是( )
| A.(-4,0) | B.(-1,0) | C.(0,2) | D.(2,0) |
如图所示为一种“羊头”形图案,其作法是:从正方形①开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形②和②,…,依此类推,若正方形①的面积为64,则正方形⑤的面积为( )

| A.2 | B.4 | C.8 | D.16 |
勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,∠BAC=90°,AB=3,AC=4,点D,E,F,G,H,I都在矩形KLMJ的边上,则矩形KLMJ的面积为( )

| A.90 | B.100 | C.110 | D.121 |
甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米,先到终点的人原地休息.已知甲先出发2秒.在跑步过程中,甲、乙两人之间的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,给出以下结论:①a=8;②b=92;③c=123.其中正确的是( )

| A.②③ | B.①②③ | C.①② | D.①③ |
如图,已知一次函数y=ax+b和正比例函数y=kx的图象交于点P,则根据图象可得二元一次方程组 的解是 .
的解是 .

如图,长方体的底面边长分别为1cm 和3cm,高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要 cm.

计算:
(1)(-3)0×6- +|π-2|-(
+|π-2|-( )-2
)-2
(2)2 +
+ -
-
(3) ×
× -
-
(4)(2 +3)2011(2
+3)2011(2 -3)2012-4
-3)2012-4 -
- .
.
如图,大拇指与小拇指尽量张开时,两指尖的距离称为指距.某项研究表明,一般情况下人的身高h是指距d的一次函数.下表是测得的指距与身高的一组数据:
| 指距d(cm) |
20 |
21 |
22 |
23 |
| 身高h(cm) |
160 |
169 |
178 |
187 |

(1)求出h与d之间的函数关系式;(不要求写出自变量d的取值范围)
(2)某人身高为196cm,一般情况下他的指距应是多少?
如图,矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD.
(1)求证:OP=OF;
(2)求AP的长.
在平面直角坐标系中,点A的坐标是(0,3),点B在x轴上,将△AOB绕点A逆时针旋转90°得到△AEF,点O,B对应点分别是E,F.
(1)若点B的坐标是(-4,0),请在图中画出△AEF,并写出点E,F的坐标;
(2)点P为x轴上的一个动点,是否存在P使PA+PE的值最小?若不存在,请说明理由,若存在请求出点P的坐标.
兰新铁路的通车,圆了全国人民的一个梦,坐上火车去观赏青海门源百里油菜花海,感受大美青海独特的高原风光,暑假某校准备组织学生、老师到门源进行社会实践,为了便于管理,师生必须乘坐在同一列高铁上,根据报名人数,若都买一等座单程火车票需2340元,若都买二等座单程火车票花钱最少,则需1650元:
西宁到门源的火车票价格如下表
| 运行区间 |
票价 |
|
|
| 上车站 |
下车站 |
一等座 |
二等座 |
| 西宁 |
门源 |
36元 |
30元 |
(1)参加社会实践的学生、老师各有多少人?
(2)由于各种原因,二等座火车票单程只能买x张(参加社会实践的学生人数<x<参加社会实践的总人数),其余的须买一等座火车票,在保证每位参与人员都有座位坐并且总费用最低的前提下,请你写出购买火车票的总费用(单程)y与x之间的函数关系式.


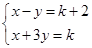 的解适合方程x+y=2,则k值为( )
的解适合方程x+y=2,则k值为( )

 <b,且a、b是两个连续的整数,则ab= .
<b,且a、b是两个连续的整数,则ab= .
 粤公网安备 44130202000953号
粤公网安备 44130202000953号