(本题9分)如图,正方形ABCD(四条边相等,四个角是直角)的边长为7cm,点M在边DC上,且CM=2cm,过点M作 ME⊥DC,交BD于点E.,动点P从点D出发沿DC边向M点运动,速度为每秒2 cm,当动点P到达M点时,运动停止.连接EP,EC.在此过程中,设P点运动时间为t秒.
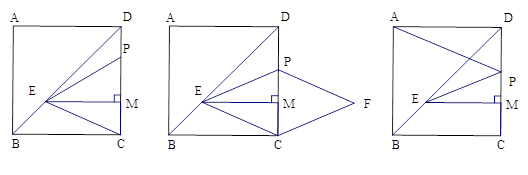
(1)EM = cm,
PC = cm(用含t的代数式表示),
当t = 秒时,△EPC的面积为15?
(2)将△EPC沿CP翻折后,点E的对应点为F点,若PF∥EC,则△EPC为 三角形,请说明理由并求此时t为何值.
(3)是否存在某一时刻,使得P点到A点、E点的距离之和最短?如果存在,直接写出PA+PE的最小值,如果不存在,请说明理由.
推荐套卷
 校区,初中部在
校区,初中部在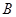 校区,学校学生会计划在3月12日植树节当天安排部分学生到郊区公园参加植树活动.已知
校区,学校学生会计划在3月12日植树节当天安排部分学生到郊区公园参加植树活动.已知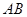 是
是 的直径,
的直径,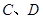 是
是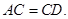


 将四边形
将四边形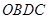 分成面积相等的两个三角形,试确定四边形
分成面积相等的两个三角形,试确定四边形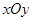 中,半径为1的圆的圆心
中,半径为1的圆的圆心 在坐标原点,且与两坐标轴分别交于
在坐标原点,且与两坐标轴分别交于 四点.抛物线
四点.抛物线 与
与 轴交于点
轴交于点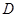 ,与直线
,与直线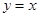 交于点
交于点 ,且
,且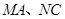 分别与圆
分别与圆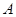 和点
和点 .
. 轴于点
轴于点 ,连结
,连结 ,并延长
,并延长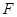 ,求
,求 的长.
的长.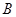 作圆
作圆 的延长线于点
的延长线于点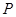 ,判断点
,判断点
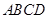 中,
中, ,且
,且 .取
.取 的中点
的中点 ,连结
,连结 .
.
 的形状;
的形状; 上,是否存在点
上,是否存在点 ,使
,使 .若存在,请求出
.若存在,请求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由. 粤公网安备 44130202000953号
粤公网安备 44130202000953号