江苏省无锡市崇安区九年级上学期期中考试数学试卷
某厂1月份生产原料a吨,以后每个月比前一个月增产x%,3月份生产原料的吨数是( )
A. |
B. |
C. |
D. |
⊙O的直径为9,圆心O到直线l的距离为6,则直线l与⊙O的位置关系是( )
| A.相交 | B.相切 | C.相离 | D.无法确定 |
下列说法正确的是( )
| A.等弧所对的圆心角相等 |
| B.三角形的外心到这个三角形的三边距离相等 |
| C.经过三点可以作一个圆 |
| D.相等的圆心角所对的弧相等 |
如图,⊙O的直径 AB=12,CD是⊙O 的弦,CD⊥AB于P,且 BP :AP=1 :5,则CD的长为( )

A. |
B. |
C. |
D. |
如图,半径为5的⊙A经过点C和点O ,点B是y轴右侧⊙A的优弧上一点,∠OBC=30º,则点C的坐标为( )

| A.(0,5) | B.(0, ) ) |
C.(0, ) ) |
D.(0, ) ) |
我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”.如图,直线l: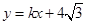 与x轴、y轴分别交于A、B,∠OAB=30º,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是( )
与x轴、y轴分别交于A、B,∠OAB=30º,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是( )
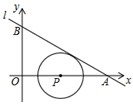
A.6 B.8 C.10 D.12
如图,半径为3的⊙P在第一象限,动点A沿着⊙P运动一周,在点A运动的同时,作点A关于原点O的对称点B,再以AB为边作等边△ABC,点C在第二象限,点C 随点A运动所形成的图形的面积为( )

A. |
B. |
C. |
D. |
如图,AB是⊙O的直径,点D在AB的延长线上,过点D作⊙O的切线,切点为C, 若∠A=25º,则∠D= .

已知 P为⊙O 外一点,PA、PB 分别切⊙O 于点 A.B,∠APB=50°,C为⊙O 上一点(不与点 A、B重合),则∠ACB 的度数为 .
李老师自制圆锥教具,已经用一个圆心角为90º、半径为4分米的扇形围成了圆锥的侧面,还需用一个半径为 分米的圆来做这个圆锥的底面圆.
如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=5,AD=4,则AE的长为 .

如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,点D为AC边上的动点,点D从点C出发,沿边CA往A运动,当运动到点A时停止,若设点D运动的时间为t秒,点D运动的速度为每秒2个单位长度.当t= 时,△CBD是等腰三角形.

如图,四边形ABCD为菱形,M为BC上一点,连接AM,交对角线BD于点G,并且∠ABM=2∠BAM.
(1)求证:AG=BG;
(2)若点M为BC的中点,同时S△BMG=1,求△ADG的面积.
如图,菱形OABC的顶点A的坐标为(2,0),∠COA=60º,将菱形OABC绕坐标原点O逆时针旋转120º得到菱形ODEF.

(1)直接写出点F的坐标;
(2)求线段OB的长及图中阴影部分的面积.
水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤.通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤.为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
已知,在△ABC中,AD为∠BAC的平分线,点E在BC的延长线上,且∠EAC=∠B,以DE为直径的半圆交AD于点F,交AE于点M.
(1)判断AF与DF的数量关系,并说明理由;
(2)只用无刻度的直尺画出△ADE的边DE上的高AH;
(3)若EF=4,DF=3,求DH的长.
问题提出:如图1,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,⊙C半径为2,P为圆上一动点,连结AP,BP,求AP+ BP的最小值.
BP的最小值.

尝试解决:为了解决这个问题,下面给出一种解题思路:如图2,连接CP,在CB上取点D,使CD=1,则有 =
= ,又∵∠PCD=∠BCP,∴△PCD∽△BCP,∴
,又∵∠PCD=∠BCP,∴△PCD∽△BCP,∴ =
= ,∴PD=
,∴PD= BP,∴AP+
BP,∴AP+ BP=AP+PD.
BP=AP+PD.
请你完成余下的思考,并直接写出答案:AP+ BP的最小值为 .
BP的最小值为 .
自主探索:在“问题提出”的条件不变的情况下,  AP+BP的最小值为 .
AP+BP的最小值为 .
拓展延伸:已知扇形COD中,∠COD=90º,OC=6,OA=3,OB=5,点P是 上一点,求2PA+PB的最小值.
上一点,求2PA+PB的最小值.
(1)阅读下列材料,求函数 的最大值.
的最大值.
解:将原函数转化成关于x的方程,得 .
.
当y=3时,为一元一次方程 ,得
,得 ;
;
当y≠3时,为一元二次方程,∵x为实数,∴△= ,∴y≤4且y≠3.
,∴y≤4且y≠3.
综上所述,y的取值范围是y≤4,即y的最大值为4.
根据材料给你的启示,求函数 的最小值.
的最小值.
(2)如图所示,酒店大堂一吊灯的下圆环直径为 米,通过拉链悬挂在天花板上,圆环呈水平状态,并且与天花板的距离(即OB)为2米.在圆环上设置三个等分点A1、A2、A3,点C为OB上一点(不与端点O、B重合),同时点C与点A1、A2、A3和点B均用拉链相连结,且CA1、CA2、CA3的长度相等.要使拉链的总长最短,BC应为多长?
米,通过拉链悬挂在天花板上,圆环呈水平状态,并且与天花板的距离(即OB)为2米.在圆环上设置三个等分点A1、A2、A3,点C为OB上一点(不与端点O、B重合),同时点C与点A1、A2、A3和点B均用拉链相连结,且CA1、CA2、CA3的长度相等.要使拉链的总长最短,BC应为多长?
 是一元二次方程,则m的值是( )
是一元二次方程,则m的值是( )
 配方后可变形为( )
配方后可变形为( )



 没有实数根,则m的取值范围是( )
没有实数根,则m的取值范围是( )



 的解是 .
的解是 . 的一个根是0,则m的值为 .
的一个根是0,则m的值为 .





 有两个实数根
有两个实数根 、
、 ,并且满足
,并且满足 ,求m的值.
,求m的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号