如图，长方形纸片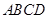
中，AB=10，将纸片折叠，使顶点
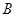落在边
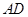上的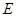
点处，折痕的一端
点在边
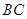上．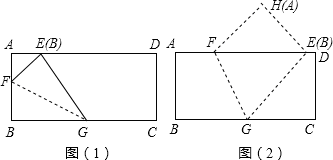
（1）如图（1），当折痕的另一端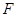
在
边上且AE=5时，求AF的长
（2）如图（2），当折痕的另一端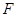在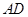边上且BG=13时，求AF的长．
（m为整数且m>1）
、
、
、
，________，__________；
，求
的值.相关知识点
推荐套卷
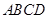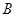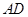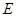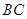如图，长方形纸片中，AB=10，将纸片折叠，使顶点落在边上的点处，折痕的一端点在边上．
（1）如图（1），当折痕的另一端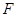在边上且AE=5时，求AF的长
（2）如图（2），当折痕的另一端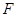在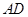边上且BG=13时，求AF的长．
粤公网安备 44130202000953号