浙江省乐清市育英寄宿学校八年级实验B班9月月考数学试卷
关于 的方程
的方程 (
( 为常数)有两个相等的实数根,那么k的值为( )
为常数)有两个相等的实数根,那么k的值为( )
A. |
B. |
C. |
D. |
已知一组数据3,7,9,10,x,12的众数是9,则这组数据的中位数是( )
| A.9 | B.9.5 | C.3 | D.12 |
下列命题中,真命题是( )
| A.四边相等的四边形是正方形 |
| B.对角线相等的菱形是正方形 |
| C.正方形的两条对角线相等,但不互相垂直平分 |
| D.矩形、菱形、正方形都具有“对角线相等”的性质 |
某农机厂四月份生产零件50万个,第二季度共生产零件182万个.设该厂第二季度平均每月的增长率为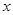 ,那么
,那么 满足的方程是( )
满足的方程是( )
A.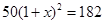 |
B.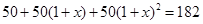 |
C.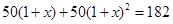 |
D.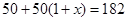 |
如图, ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的边长为( )
ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的边长为( )

A.2 |
B.4 |
C.4 | D.8 |
如图,把一个长方形的纸片按图示对折两次,然后剪下一部分,为了得到一个钝角为120°的菱形,剪口与第二次折痕所成角的度数应为( )

| A.15°或30° | B.30°或45° | C.45°或60° | D.30°或60° |
如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )

| A.1 | B. |
C.4﹣2 |
D.3 ﹣4 ﹣4 |
在等腰△ABC中,∠ACB=90°,且AC=1.过点C作直线l∥AB,P为直线l上一点,且AP=AB.则点P到BC所在直线的距离是( )
A.1 B.1或 C.1或
C.1或 D.
D. 或
或
已知关于x的一元二次方程 的两个实数根分别为α、β,则(α+3)(β+3)=______.
的两个实数根分别为α、β,则(α+3)(β+3)=______.
如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是 .

△ABC中,AB=3,AC=4,BC=5,△ABD、△ACE、△BFC都是等边三角形。则四边形ADEF的面积为 .

有下列4个命题:①方程x2﹣( +
+ )x+
)x+ =0的根是
=0的根是 和
和 .②在△ABC中,∠ACB=90°,CD⊥AB于D.若AD=4,BD=
.②在△ABC中,∠ACB=90°,CD⊥AB于D.若AD=4,BD= ,则CD=3.③点P(x,y)的坐标x,y满足x2+y2+2x﹣2y+2=0,且xy=k,则k=﹣1.④如图,折叠矩形纸片ABCD,使B点落在AD上一点E处,折痕的两端点分别在AB、BC上(含端点),且AB=6,BC=10。设AE=x,则x 的取值范围是2≤x≤6.上述4个命题中,真命题的序号是 .
,则CD=3.③点P(x,y)的坐标x,y满足x2+y2+2x﹣2y+2=0,且xy=k,则k=﹣1.④如图,折叠矩形纸片ABCD,使B点落在AD上一点E处,折痕的两端点分别在AB、BC上(含端点),且AB=6,BC=10。设AE=x,则x 的取值范围是2≤x≤6.上述4个命题中,真命题的序号是 .

如图,矩形 中,
中, ,点
,点 是
是 边上一点,连接
边上一点,连接 ,把
,把 沿
沿 折叠,使点
折叠,使点 落在点
落在点 处,当△
处,当△ 为直角三角形时,
为直角三角形时, 的长为
的长为

如图,在□ABCD中,F是AD的中点,延长BC到点E,使CE= BC,连结DE,CF。
BC,连结DE,CF。
(1)求证:四边形CEDF是平行四边形;
(2)若AB=4,AD=6,∠B=60°,求DE的长。
为了解学生零花钱的使用情况,校团委随机调查了本校部分学生每人一周的零花钱数额,并绘制了如图甲、乙所示的两个统计图(部分未完成).请根据图中信息,回答下列问题:
(1)校团委随机调查了多少学生?请你补全条形统计图;
(2)表示“50元”的扇形的圆心角是多少度?补调查的学生每人一周零花钱数额的中位数是多少元?
(3)四川地震后,全校1000名学生每人自发地捐出一周零花钱的一半,以支援灾区建设.请估算全校学生共捐款多少元?
四川地震后,某商家为支援灾区人民,计划捐赠帐篷16800顶,该商家备有2辆大货车、8辆小货车运送帐篷.计划大货车比小货车每辆每次多运帐篷200顶,大、小货车每天均运送一次,两天恰好运完.
(1)求大、小货车原计划每辆每次各运送帐篷多少顶?
(2)因地震导致路基受损,实际运送过程中,每辆大货车每次比原计划少运200m顶,每辆小货车每次比原计划少运300m顶,为了尽快将帐篷运送到灾区,大货车每天比原计划多跑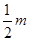 次,小货车每天比原计划多跑m次,一天恰好运送了帐篷14400顶,求m的值.
次,小货车每天比原计划多跑m次,一天恰好运送了帐篷14400顶,求m的值.
关于x的一元二次方程(a﹣6)x2﹣8x+9=0有实根.
(1)求a的最大整数值;
(2)当a取最大整数值时,①求出该方程的根;②求 的值.
的值.
如图,在直角梯形ABCD中,AD∥BC,∠B=90°,且AD=12cm,AB=8cm,DC=10cm,若动点P从A点出发,以每秒2cm的速度沿线段AD向点D运动;动点Q从C点出发以每秒3cm的速度沿CB向B点运动,当P点到达D点时,动点P、Q同时停止运动,设点P、Q同时出发,并运动了t秒,回答下列问题:

(1)BC= cm;
(2)当t为多少时,四边形PQCD成为平行四边形?
(3)当t为多少时,四边形PQCD为等腰梯形?
(4)是否存在t,使得△DQC是等腰三角形?若存在,请求出t的值;若不存在,说明理由.
 的方程
的方程 的一个根是1,则代数式
的一个根是1,则代数式 的值等于( )
的值等于( )





 ,且一元二次方程kx2+ax+b=0有两个实数根,则k的取值范围是 .
,且一元二次方程kx2+ax+b=0有两个实数根,则k的取值范围是 . 的值为8,则代数式
的值为8,则代数式 的值为
的值为 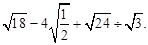
 粤公网安备 44130202000953号
粤公网安备 44130202000953号