初中数学圆内接四边形的性质解答题

（本题10分）已知：如图，□ABCD的对角线AC的垂直平分线与边AD、BC分别交于E、F．
求证：四边形AFCE是菱形．

（本题12分）如图，在平行四边形ABCD中，E、F分别在AD、BC边上，且AE=CF．

求证：（1）△ABE≌△CDF；
（2）四边形BFDE是平行四边形．

（本小题满分8分）如图，E、F分别为□ABCD对角线BD上的点，且BE=DF．
求证：AE=CF．

已知：如图，在矩形ABCD中，M，N分别是边AD， BC的中点，E，F分别是线段BM，CM的中点．

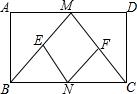
（1）求证：△ABM≌△DCM；
（2）判断四边形MENF是什么特殊四边形，并证明你的结论；
（3）当AD：AB=            时，四边形MENF是正方形（只写结论，不需证明）．

（本题10分）已知，点I是△ABC的内心（三角形三个内角平分线的交点），过点B作BP⊥BI交AI的延长线于点P．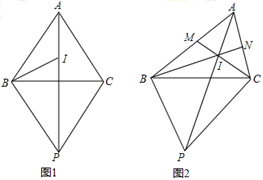

（1）如图1，若BA＝BC,
①求证：BP∥AC；
②设∠BAC＝α（其中α为常数），求∠BCP；
（2）如图2，CM、BN为△ABC的角平分线，若BM＋CN＝6，∠BAC＝60°，请你直接写出点P到直线BC的距离的最大值等于___________．

（本题8分）如图，已知矩形ABCD，点E为BC的中点，将△ABE沿直线AE折叠，点B落在B′点处，连接B′C．

（1）求证：AE∥B′C；
（2）若AB＝4，BC＝6，求线段B′C的长．

（本小题满分8分）如图所示，折叠长方形一边AD，点D落在BC边的点F处，已知BC=10厘米，AB=8厘米，求FC和EF的长。
 

（本小题满分8分）如图，在平行四边形ABCD中，点E、F在对角线BD上，且BE=DF，
四边形AECF是平行四边形吗？为什么？

看图回答问题：

（1）内角和为2014°，小明为什么说不可能？
（2）小华求的是几边形的内角和？
（3）错把外角当内角的那个外角的度数你能求出来吗？它是多少度？

一个多边形的外角和是内角和的，求这个多边形的边数．

如图，已知：E，F是平行四边形ABCD对角线BD上的两点，且BE=DF。
求证：四边形AECF是平行四边形。

如图（1），已知正方形ABCD的对角线AC、BD相交于点O，E是AC上一点，连结EB，过点A作AM⊥BE，垂足为M，AM交BD于点F．

（1）试说明OE＝OF；
（2）如图（2），若点E在AC的延长线上，AM⊥BE于点M，交DB的延长线于点F，其它条件不变，则结论“OE＝OF”还成立吗?如果成立，请给出说明理由；如果不成立，请说明理由．

如图，△ABC中，点O是边AC上一个动点，过O作直线MN∥BC．设MN交∠ACB的平分线于点E，交∠ACB的外角平分线于点F．

（1）求证：OE=OF；
（2）若CE=12，CF=9，求OC的长；
（3）当点O在边AC上运动到什么位置时，四边形AECF是矩形？并说明理由．

如图，在∠ABC中，AB = BC，D、E、F分别是BC、AC、AB边上的中点；

（1）求证：四边形BDEF是菱形；
（2）若AB = ，求菱形BDEF的周长．

已知：如图，把矩形纸片ABCD沿EF折叠后．点D与点B重合，点C落在点C′的位置上．若∠1＝60°，AE=1．

（1）求∠2、∠3的度数；
（2）求矩形纸片ABCD的面积S．