广东省广州市南沙区八年级下学期期末学业水平测试数学试卷
在□ABCD中,AB=3,BC=4,则CD等于( )
| A.2 | B.3 | C.4 | D.5 |
2015年广州将举办以“从小不浪费”为主题的第九届羊城“小市长”评选系列活动,我区通过初选从11名同学抽选最好成绩的6名同学去参加决赛,他们的决赛成绩各不相同,其中小明知道自己的成绩,但能否参加决赛,他还必须要清楚这11名同学成绩的( )
| A.平均数 | B.众数 | C.中位数 | D.方差 |
在△ABC中,如果三边满足关系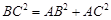 ,则△ABC的直角是( )
,则△ABC的直角是( )
| A.∠A | B.∠B | C.∠C | D.不能确定 |
如图,在 中,E、F分别是边AC、BC的中点,且DF//AC,BD=3,则EF的长为( )
中,E、F分别是边AC、BC的中点,且DF//AC,BD=3,则EF的长为( )

A.2 B.3 C.4 D.5
已知一次函数 中,
中, 随着
随着 的增大而减小,则这个函数的图像不经过( )
的增大而减小,则这个函数的图像不经过( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
星期天,小明参加南沙自行车协会组织的“南沙横琴骑行游”活动,早上8:00出发骑车从南沙前往珠海横琴.2小时后,爸爸骑摩托车沿同一线路也从南沙前往横琴,他们的行驶路程 (千米)与小明的行驶时间
(千米)与小明的行驶时间 (小时)之间的函数关系如图所示,下列说法不正确的是( )
(小时)之间的函数关系如图所示,下列说法不正确的是( )

| A.南沙与横琴两地相距60千米 |
| B.11:00时,爸爸和小明在途中相遇 |
| C.爸爸骑摩托车的平均速度是60千米/小时 |
| D.爸爸比小明早到横琴1小时 |
如图,五根小木棒的长度分别为7,15,20,24,25,现将它们摆成两个直角三角形,其中正确的是( )

如图,菱形ABCD的边长为6, ,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是( )
,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是( )

| A.6 | B. |
C. |
D. |
如表是某校男子篮球队队员的年龄(单位:岁)分布:
| 年龄 |
14 |
15 |
16 |
17 |
18 |
| 人数 |
1 |
4 |
3 |
2 |
2 |
则该校男子篮球队队员的年龄的众数为 岁.
如图,由于台风的影响,一棵树在离地面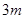 处折断,树顶落在离树干底部
处折断,树顶落在离树干底部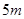 处,则这棵树在折断前(不包括树根)的长度是
处,则这棵树在折断前(不包括树根)的长度是 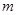 .
.
如图,顺次连接矩形 四边的中点得到四边形
四边的中点得到四边形 ,然后顺次连接四边形
,然后顺次连接四边形 的中点得到四边形
的中点得到四边形 ,再顺次连接四边形
,再顺次连接四边形 四边的中点得到四边形
四边的中点得到四边形 ,…,已知
,…,已知 ,按此方法得到的四边形
,按此方法得到的四边形 的周长为 .
的周长为 .

(本小题满分8分)如图,E、F分别为□ABCD对角线BD上的点,且BE=DF.
求证:AE=CF.
(本小题满分8分)为了从甲、乙两名选手中选拔一个参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶6次,命中的环数如下(单位:环):
甲:7,8,8,6,10,9 乙:9,6,7,8,9,9
(1)求甲、乙两名选手的射击平均成绩分别是多少?
(2)如果你是教练,你会派哪一位选手参加比赛?请说明理由.
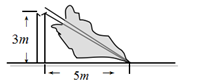
(本小题满分8分)如图,梯子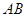 斜靠在一竖直的墙上,梯子的底端
斜靠在一竖直的墙上,梯子的底端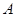 到墙根
到墙根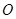 的距离
的距离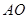 为2米,梯子的顶端B到地面的距离
为2米,梯子的顶端B到地面的距离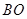 为6米.现将梯子的底端
为6米.现将梯子的底端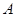 向外移动到
向外移动到 ,使梯子的底端
,使梯子的底端 到墙根
到墙根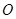 的距离
的距离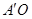 等于3米,同时梯子的顶端
等于3米,同时梯子的顶端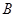 下降至
下降至 .求梯子顶端下滑的距离
.求梯子顶端下滑的距离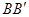 .
.
(本小题满分8分)如图,已知一次函数 与正比例函数
与正比例函数 图像相交于点A
图像相交于点A  ,
, 与
与 轴交于点B.
轴交于点B.
(1)求出m、n的值;
(2)求出 的面积.
的面积.
(本小题满分8分)如图,在正方形ABCD中,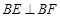 ,
,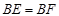 ,EF交BC于点G.
,EF交BC于点G.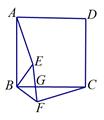
(1)求证: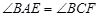 ;
;
(2)若 ,求
,求 的大小.
的大小.
(本小题满分10分)某班组织学生到百万葵园进行户外学习活动,已知百万葵园的门票销售分两类:一类为散客门票,票价每张120元;另一类为团体门票(一次性购买门票20张以上),每张门票价格在散客门票价格基础上打8折,设本次活动共有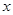 人参加,购买门票需要
人参加,购买门票需要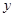 元.
元.
如果都买散客票,求y与x之间的函数关系式;
如果买团体票,求y与x之间的函数关系式,并写出自变量的取值范围;
请根据人数变化设计一种比较省钱的购票方案.
 在实数范围内有意义,则
在实数范围内有意义,则 的取值范围是( )
的取值范围是( )







 .
. 的图象经过点(
的图象经过点( ,
, ),则
),则 的值为 .
的值为 . ,∠ABC=45°,则点D的坐标为 .
,∠ABC=45°,则点D的坐标为 .
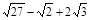
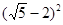
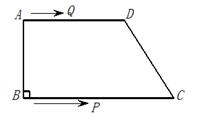
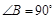 ,AD=8cm,BC=10cm,
,AD=8cm,BC=10cm,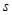 ).
).
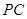 = ;(用含t的式子表示)
= ;(用含t的式子表示)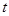 为何值时,
为何值时, 是等腰三角形?
是等腰三角形? 粤公网安备 44130202000953号
粤公网安备 44130202000953号