如图,在平行四边形ABCD中,∠ABD=30°，AB=4，BD=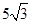
，将△BCD沿
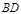方向平移，得到△EFG．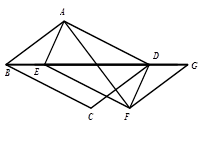
（1）连结AE、DF，求证：四边形AEFD为平行四边形．
（2）若□AEFD为矩形，求△BCD平移的距离BE．
=
相关知识点
推荐套卷
如图,在平行四边形ABCD中,∠ABD=30°，AB=4，BD=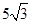，将△BCD沿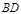方向平移，得到△EFG．
（1）连结AE、DF，求证：四边形AEFD为平行四边形．
（2）若□AEFD为矩形，求△BCD平移的距离BE．
粤公网安备 44130202000953号