初中数学圆内接四边形的性质解答题

如图，四边形ABCD是长方形．

（1）作△ABC关于直线AC对称的图形；
（2）试判断（1）中所作的图形与△ACD重叠部分的三角形形状，并说明理由．

（1）如图1，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE．求证：CE=CF；
（2）如图2，在正方形ABCD中，E是AB上一点，G是AD上一点，如果∠GCE=45°，请你利用（1）的结论证明：GE=BE+GD．
（3）运用（1）（2）解答中所积累的经验和知识，完成下题：
如图3，在直角梯形ABCD中，AD∥BC（BC＞AD），∠B=90°，AB=BC，E是AB上一点，且∠DCE=45°，BE=4，DE=10，求直角梯形ABCD的面积．

如图，在▱ABCD中，E、F分别为边ABCD的中点，BD是对角线，过A点作平行四边形AGDB交CB的延长线于点G．

（1）求证：DE∥BF；
（2）若∠G=90，求证：四边形DEBF是菱形．

如图，将▱ABCD的边DC延长到点E，使CE=DC，连接AE，交BC于点F．

（1）求证：△ABF≌△ECF；
（2）若∠AFC=2∠D，连接AC、BE，求证：四边形ABEC是矩形．

已知，矩形ABCD中，AB=4cm，BC=8cm，AC的垂直平分线EF分别交AD、BC与点E、F，垂足为O．

（1）如图1，连接AF、CE．求证四边形AFCE为菱形，并求AF的长；
（2）如图2，动点P、Q分别从A、C两点同时出发，沿△AFB和△CDE各边匀速运动一周，即点P自A→F→B→A停止，点Q自C→D→E→C停止，在运动过程中，已知点P的速度为每秒5cm，点Q的速度为每秒4cm，运动时间为t秒，当A、C、P、Q四点为顶点的四边形是平行四边形时，求t的值．

如图，在Rt△ABC中，∠B=90°，AC=60cm，∠A=60°，点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动，同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t秒（0＜t≤15）．过点D作DF⊥BC于点F，连接DE，EF．

（1）求证：AE=DF；
（2）四边形AEFD能够成为菱形吗？如果能，求出相应的t值，如果不能，说明理由；
（3）当t为何值时，△DEF为直角三角形？请说明理由．

在平行四边形ABCD中，对角线AC和BD交于点O，AC=8．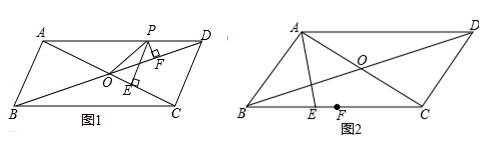

（1）如图1，若AB⊥AC，BD=12，点P是线段AD上的动点（不包含端点A，D），过点P作PE⊥AC，垂足为点E，PF⊥BD，垂足为点F，设PE=x，PF=y，求y与x的函数关系式并直接写出自变量x的取值范围；
（2）如图2，若AE平分∠BAC，点F为BC中点，且点F保持在点E的右边，求线段BC的变化范围．

如图，在四边形ABCD中，∠ABC=90°，∠BAD=135°，AB=1，AC=，点E为CD中点．
求证：CD=2AE．

如图，在正方形ABCD中，点E是对角线BD上的点，求证：△ABE≌△CBE．

观察下列图形的变化过程，解答以下问题：
如图，在△ABC中，D为BC边上的一动点（D点不与B、C两点重合）．DE∥AC交AB于E点，DF∥AB交AC于F点．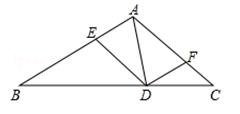

（1）试探索AD满足什么条件时，四边形AEDF为菱形，并说明理由；
（2）在（1）的条件下，△ABC满足什么条件时，四边形AEDF为正方形．为什么？

已知：在平面直角坐标系中，点A（1，0），点B（4，0），点C在y轴正半轴上，且OB=2OC．
（1）试确定直线BC的解析式；
（2）在平面内确定点M，使得以点M、A、B、C为顶点的四边形是平行四边形，请直接写出点M的坐标．

如图，已知△ABC中，AB=2，BC=4

（1）画出△ABC的高AD和CE；
（2）若AD=，求CE的长．

如图，在6×6的正方形网格中，每个小正方形的顶点称为格点，每个小正方形的边长均为1，点A，B，C都在格点上，在正方形网格中找到格点D，使以A，B，C，D为顶点的四边形是平行四边形，并画出所有符合要求的平行四边形．

如图，在▱ABCD中，对角线AC，BD相交于点O，AC+BD=36，△ABO的周长为30，求AB的长．

如图，正方形ABCD，DE与HG相交于点O．

（1）如图（1），当∠GOD=90°，①求证：DE=GH； ②求证：GD+EH≥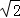DE；
（2）如图（2），当∠GOD=45°，边长AB=4，HG=2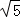，求DE的长．