（1）如图1，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE．求证：CE=CF；
（2）如图2，在正方形ABCD中，E是AB上一点，G是AD上一点，如果∠GCE=45°，请你利用（1）的结论证明：GE=BE+GD．
（3）运用（1）（2）解答中所积累的经验和知识，完成下题：
如图3，在直角梯形ABCD中，AD∥BC（BC＞AD），∠B=90°，AB=BC，E是AB上一点，且∠DCE=45°，BE=4，DE=10，求直角梯形ABCD的面积．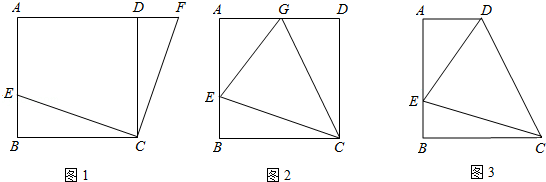
相关试题
在平面直角坐标系中，已知点A（－4,3）、B（－2,－3）
（1）描出A、B两点的位置，并连结AB、AO、BO。
（2）△AOB的面积是__________。
把△AOB向右平移4个单位，再向上平移2个单位，画出平移后的△A′B′C′，并写出各点的坐标。
并写出它的整数解
相关知识点
推荐套卷
粤公网安备 44130202000953号