福建省厦门市湖里区八年级下学期期末数学试卷
下列各式中,y随x的变化关系式是正比例函数的是( )
| A.y="2x" | B.y= |
C.y=x﹣1 | D.y=x2﹣1 |
如图,在直角三角形ABC中,∠B=90°,以下式子成立的是( )
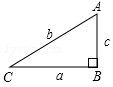
| A.a2+b2=c2 | B.a2+c2=b2 | C.b2+c2=a2 | D.(a+c)2=b2 |
下列四边形对角线相等但不一定垂直的是( )
| A.平行四边形 | B.矩形 | C.菱形 | D.正方形 |
如图,特殊四边形的面积表达式正确的是( )
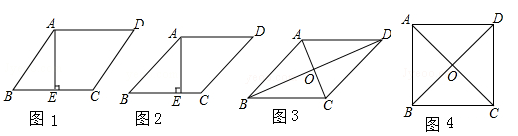
A.如图1,平行四边形ABCD中,AE⊥BC,则平行四边形ABCD的面积为: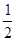 BC×AE BC×AE |
B.如图2,菱形ABCD中,AE⊥BC,则菱形ABCD的面积为: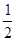 BC×AE BC×AE |
| C.如图3,菱形ABCD中,对角线交于点O,则菱形ABCD的面积为:AC×BD |
D.如图4,正方形ABCD中,对角线交于点O,则正方形ABCD的面积为: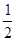 AC×BD AC×BD |
以下四点:(1,2),(2,3),(0,1),(﹣2,3)在直线y=2x+1上的有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
已知平行四边形ABCD的对角线交于点O,则下列命题是假命题的是( )
| A.若AC⊥BD,则平行四边形ABCD是菱形 |
| B.若BO=2AO,则平行四边形ABCD是菱形 |
| C.若AB=AD,则平行四边形ABCD是菱形 |
| D.若∠ABD=∠CBD,则平行四边形ABCD是菱形 |
将一组数据:3,1,2,4,2,5,4去掉3后,新的数据的特征量发生变化的是( )
| A.中位数 | B.平均数 | C.众数 | D.方差 |
已知点O为平面直角坐标系的原点,点A(5,0),点B(x,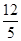 ),若△AOB是直角三角形,则x取值有( )
),若△AOB是直角三角形,则x取值有( )
| A.4个 | B.3个 | C.2个 | D.1个 |
在一次芭蕾舞比赛中,甲、乙两个芭蕾舞团都表演了舞剧《天鹅湖》,甲、乙参加表演的8个女演员身高的方差分别为S甲2=1.5,S乙2=2.5,则 芭蕾舞团的身高更整齐(填“甲”或“乙”).
初二(1)班共有50个人,期中考数学成绩有5个人不合格,初二年段共有600名学生,各个班级数学学习水平相差不大,请你估计年段数学不及格的人数大约有 人.
如图,平行四边形OABC的顶点O,A,C的坐标分别是(0,0),(3,0),(1,2),则顶点B的坐标是 .

若直线y1上的每个点都可以表示为( m﹣2,m),且直线y1和y轴交点为点A,和直线y2=x交点为点B,若点O为坐标原点,则△AOB的面积为 .
m﹣2,m),且直线y1和y轴交点为点A,和直线y2=x交点为点B,若点O为坐标原点,则△AOB的面积为 .
某公司需招聘一名公关人员.对甲、乙两位应试者进行了面试和笔试,他们的成绩(百分制)如表所示.公司规定,面试成绩与笔试成绩的权重分别为6和4,请计算甲、乙两人各自的平均成绩,谁将被录取?
| 应试者 |
面试 |
笔试 |
| 甲 |
80 |
90 |
| 乙 |
90 |
80 |
如图,在四边形ABCD中,AB∥CD,∠BAD=90°,AB=5,BC=12,AC=13.
求证:四边形ABCD是矩形.
甲、乙两商场春节期间都进行让利酬宾活动.其中,甲商场对一次购物中超过200元后的价格部分打7折,如图所示,表示甲商场在让利方式下y关于x的函数图象,x(单位:元)表示商品原价,y(单位:元)表示购物金额.若乙商场所有商品按8折出售,请在同一坐标系下画出乙商场在让利方式下y关于x的函数图象,并说明如何选择这两家商场购物更省钱.
在同一平面直角坐标系中,观察以下直线:y=2x,y=﹣x+6,y=x+2,y=4x﹣4图象的共同特点,若y=kx+5也有该特点,试求满足条件的k值.
如图,在四边形ABCD中,∠ABC=90°,∠BAD=135°,AB=1,AC= ,点E为CD中点.
,点E为CD中点.
求证:CD=2AE.
在平面直角坐标系中,点A,B的坐标分别为(4,0),(0,4),直线y= x+b和线段AB交于点D,DE⊥x轴,垂足为点E,DF⊥y轴,垂足为点F,记w=DF﹣DE,当1≤w≤2时,求b的取值范围.
x+b和线段AB交于点D,DE⊥x轴,垂足为点E,DF⊥y轴,垂足为点F,记w=DF﹣DE,当1≤w≤2时,求b的取值范围.
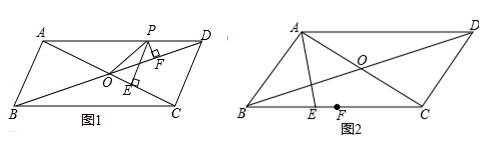
如图,四边形ABCD是菱形,CE⊥AB,垂足为点E,且CE交对角线BD于点F.若∠A=120°,四边形AEFD的面积为 ,求EF的值.
,求EF的值.
在平面直角坐标系中,直线y1= x+a和y2=﹣
x+a和y2=﹣ x+b交于点E(3,3),点P(m,n)在直线y1=
x+b交于点E(3,3),点P(m,n)在直线y1= x+a上,过点P(m,n)作x轴的垂线,交直线y2=﹣
x+a上,过点P(m,n)作x轴的垂线,交直线y2=﹣ x+b于点F.
x+b于点F.
(1)若n=2,求△PEF的面积;
(2)若PF=2,求点P的坐标.
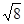 的结果是( )
的结果是( )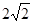
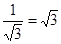
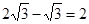
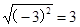
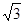 )2=6
)2=6 在实数范围内有意义,则x的取值范围是 .
在实数范围内有意义,则x的取值范围是 .
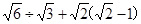

 粤公网安备 44130202000953号
粤公网安备 44130202000953号