贵州省黔南州八年级下学期期末数学试卷
已知 =0,那么(a+b)2015的值为( )
=0,那么(a+b)2015的值为( )
| A.﹣1 | B.1 | C.52015 | D.﹣52015 |
已知点(﹣2,y1),(﹣1,y2),(1,y3)都在直线y=﹣3x+2上,则y1,y2,y3的大小关系是( )
| A.y1>y2>y3 | B.y1<y2<y3 |
| C.y3>y2>y1 | D.y3<y2<y1 |
如图,在▱ABCD中,CD=3,AD=5,AE平分交∠BAD边于点E,则线段BE,CE的长分别是( )

| A.2和3 | B.3和2 | C.4和1 | D.1和4 |
正方形具备而菱形不具备的性质是( )
| A.四条边都相等 | B.四个角都是直角 |
| C.对角线互相垂直平分 | D.每条对角线平分一组对角 |
如图,正方形的边长为4cm,则图中阴影部分的面积为( )cm2.

| A.8 | B.16 | C.4 | D.无法确定 |
甲、乙两人在一次百米赛跑中,路程s(米)与赛跑时间t(秒)的关系如图所示,则下列说法正确的是( )

| A.甲、乙两人的速度相同 | B.甲先到达终点 |
| C.乙用的时间短 | D.乙比甲跑的路程多 |
甲、乙两班举行电脑汉字输入比赛,参赛学生每分钟输入汉字的个数统计结果如下表:

某同学分析上表后得出如下结论:
(1)甲、乙两班学生成绩平均水平相同;
(2)乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字≥150个为优秀);
(3)甲班成绩的波动比乙班大,
上述结论正确的是( )
| A.(1)(2)(3) | B.(1)(2) | C.(1)(3) | D.(2)(3) |
如图,在菱形ABCD中,对角线AC、BD相交于点O,E为CD的中点,则下列式子中不一定成立的是( )

A.BC="2OE" B.CD="2OE" C.CE="OE" D.OC=OE
如图,直线l上有三个正方形A、B、C,若正方形A、C的面积分别为5和11,则正方形B的面积为( )

A.4 B.6 C.16 D.55
若点E,F,G,H分别是菱形ABCD的边AB,BC,CD,DA的中点,则四边形EFGH的形状为 .
如图所示,在▱ABCD中,E,F分别为AD,BC边上的一点,若添加一个条件 ,则四边形EBFD为平行四边形.

长方形纸片ABCD中,AD=4cm,AB=10cm,按如图方式折叠,使点B与点D重合,折痕为EF,求DE的长.
如图,在平行四边形ABCD中,AC是它的一条对角线,BE⊥AC于点E,DF⊥AC于点F,求证:四边形BEDF是平行四边形.
某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了15人某月的加工零件个数:
(1)写出这15人该月加工零件数的平均数、中位数和众数.
(2)假如生产部负责人把每位工人的月加工零件数定为260(件),你认为这个定额是否合理,为什么?
如图,某会展中心在会展期间准备将高5m,长13m,宽2m的楼梯上铺地毯,已知地毯每平方米18元,请你帮助计算一下,铺完这个楼道至少需要多少元钱?
如图,在平四边形ABCD中,对角线AC与BD相交于点O,P为线段BC上一点(除端点外),连接PO并延长交AD于点Q,延长BC到点E,使CE=BC,连接DE.
(1)求证:BP=DQ;
(2)已知AB=5,AC=6,若CD= BE,求△BDE的周长.
BE,求△BDE的周长.
甲市火车货运站现有苹果1530吨,梨1150吨,安排一列货车将这批苹果和梨运往乙市.这列货车可以挂A、B两种不同规格的货箱共50节,已知用一节A型货箱的运费是0.5万元,用一节B型货箱的运费用是.0.8万元.
(1)设运输这批苹果和梨的总运费为y(万元),用A型货箱的节数为x(节),试写出y与x的函数关系式.
(2)已知35吨苹果和15吨梨可装满一节A型货箱,25吨苹果和35吨梨可装满一节B型车箱,请问运输所有苹果和梨的方案共有几种,请设计出来.
(3)利用函数的性质说明,在第(2)问的方案中,哪种方案的运费最少,最少运费用是多少?




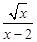 在实数范围内有意义,则x的取值范围是 .
在实数范围内有意义,则x的取值范围是 . =ad﹣bc,则
=ad﹣bc,则 = .
= .

 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号