江苏省常熟市阳光学校八年级上学期第一次月考数学试卷
如图,△ABC≌△DCB,点A、B的对应顶点分别为点D、C,如果AB=7 cm,BC=12 cm,AC=9 cm,那BD的长是( ).
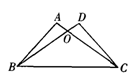
A.7cm B.9cm C.12cm D.无法确定
下列命题:
①有两个角和一个角的对边对应相等的两个三角形全等;
②有一边和一个角对应相等的两个等腰三角形全等;
③有一边对应相等的两个等边三角形全等;
④一个锐角和一条边对应相等的两个直角三角形全等.
其中是真命题的是( ).
| A.①②③ | B.①②④ |
| C.①③④ | D.②③④ |
如图,已知△ABC,求作一点P,使点P到∠A的两边的距离相等,且PA=PB.下列确定点P的方法正确的是( ).
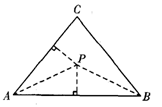
A.P为∠A、∠B两角平分线的交点
B.P为∠A的角平分线与AB的垂直平分线的交点
C.P为AC、AB两边上的高的交点
D.P为AC、AB两边的垂直平分线的交点
如图,AC、BD相交于点O,OA=OB,OC=OD,则图中全等三角形的对数是( ).
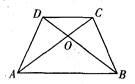
A.1对 B.2对 C.3对 D.4对
如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是( )
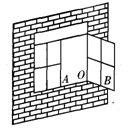
| A.三角形的稳定性 | B.两点之间线段最短 |
| C.N点确定一条直线 | D.垂线段最短 |
如图,在△ABC中,F为AC中点,E为AB上一点,D为EF延长线上一点,∠A=∠ACD,则CD与AE的关系为( ).
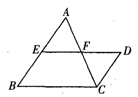
| A.相等 | B.平行 | C.平行且相等 | D.以上都不是 |
如图,∠1=∠2,AC=AD,增加下列条件:①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E.其中能使△ABC≌△AED的条件有( ).
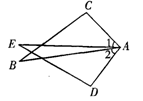
| A.4个 | B.3个 | C.2个 | D.1个 |
如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,PE、PF分别交AB、AC于点E、F.给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形;③S四边形AEPF=S△ABC;④EF=AP.当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),上述结论中始终正确的有( ).
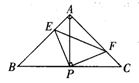
A.1个 B.2个 C.3个 D.4个
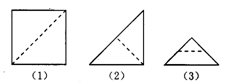
小明拿了一张正方形的纸片,如图(1),沿虚线对折一次得图(2),再对折一次得(3),然后用剪刀沿图(3)中的虚线(虚线与底、边平行)剪去一个角,打开后的形状是( ).
如图,在△ABC中,点D、E分别是边AC、BC上的点,若△ADB≌△EDB≌△EDC,AB=10 cm,则BC=_______cm.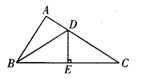
在如图所示的4×4正方形网格中,∠1+∠2+∠3+∠4+∠5+∠6+∠7=_______.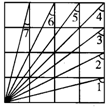
如图,△ABE和△ACD是△ABC分别沿着AB、AC边翻折180°形成的,若∠BAC=150°,则∠θ=_______.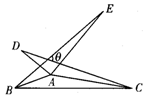
下列图形中,有一个图形不具备其他图形的共性,你认为是图形_______,(填编号)简述理由:_____________________.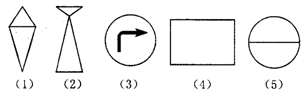
如图,△ABC是不等边三角形,DE=BC,以点D、E为两个顶点作位置不同的三角形,使所作的三角形与△ABC全等,这样的三角形最多可以画出_______个.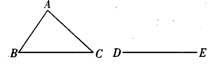
如图(1),把大小为4×4的正方形方格图形分割成两个全等图形,请在图(2)中,沿着虚线画出四种不同的分法,把4×4的正方形方格图形分割成两个全等图形.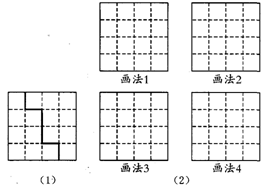
如图,点B、C在∠SAT的两边上,且AB=AC.
(1)请按下列语句用尺规画出图形.(不写画法,保留作图痕迹)
①AN⊥BC,垂足为N;
②∠SBC的平分线交AN延长线于点M;
③连接CM.
(2)该图中有_______对全等三角形.
如图,△ABO≌△CDO,点B在CD上,AO∥CD,∠BOD=30°,求∠A的度数.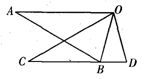
如图,已知AF=ED,AE=FD,点B、C在AD上,AB=CD.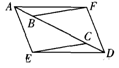
(1)写出图中所有的全等三角形;
(2)我会说明△_______≌△_______.
如图,延长△ABC的各边,使得BF=AC,AE=CD=AB,顺次连接点D、E、F,得到△DEF为等边三角形.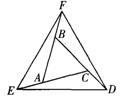
(1)试说明△AEF≌△CDE;
(2)△ABC是等边三角形吗?请说明你的理由.
如图,要用一块长4米、宽2米的长方形木板,拼接出一块长5米、宽1.5米的长方形木板,为了保证牢固,要求接缝条数尽可能地少.你能用自己学过的图形全等的有关知识设计一个拼接方案吗?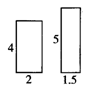

 粤公网安备 44130202000953号
粤公网安备 44130202000953号