如图1, ,分别在 的两边 , 上取点 , ,使 ,点 在 的平分线 上, 于点 ,点 在线段 上(不与点 重合),以 , 为邻边作 ,连接 , .
(1)猜想 与 之间的关系,并证明你的猜想;
(2)如图2,连接 交 于点 .
①求证: .
②若 , ,求线段 的长.

如图1,在矩形 中, 是 的中点,以点 为直角顶点的直角三角形 的两边 , 分别过点 , , .

(1)求证: ;
(2)将 绕点 按顺时针方向旋转,当旋转到 与 重合时停止转动,若 , 分别与 , 相交于点 , (如图 .
①求证: ;
②若 ,求 面积的最大值;
③当旋转停止时,点 恰好在 上(如图 ,求 的值.
边长为 的正方形 中, 是对角线 上的一个动点(点 与 、 不重合),连接 ,将 绕点 顺时针旋转 到 ,连接 , 与 交于点 , 延长线与 (或 延长线)交于点 .
(1)连接 ,证明: ;
(2)设 , ,试写出 关于 的函数关系式,并求当 为何值时, ;
(3)猜想 与 的数量关系,并证明你的结论.

如图,在正方形 中, 是对角线 与 的交点, 是 边上的动点(点 不与 , 重合), , 与 交于点 ,连接 , , .下列五个结论:① ;② ;③ ;④ ;⑤若 ,则 的最小值是 ,其中正确结论的个数是
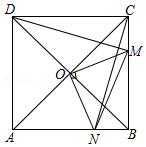
A.2B.3C.4D.5
如图1,对角线互相垂直的四边形叫做垂美四边形.
(1)概念理解:如图2,在四边形 中, , ,问四边形 是垂美四边形吗?请说明理由;
(2)性质探究:如图1,四边形 的对角线 、 交于点 , .试证明: ;
(3)解决问题:如图3,分别以 的直角边 和斜边 为边向外作正方形 和正方形 ,连接 、 、 .已知 , ,求 的长.

阅读下面的例题及点拨,并解决问题:
例题:如图①,在等边 中, 是 边上一点(不含端点 , , 是 的外角 的平分线上一点,且 .求证: .
点拨:如图②,作 , 与 的延长线相交于点 ,得等边 ,连接 .易证: ,可得 , ;又 ,则 ,可得 ;由 ,进一步可得 ,又因为 ,所以 ,即: .
问题:如图③,在正方形 中, 是 边上一点(不含端点 , , 是正方形 的外角 的平分线上一点,且 .求证: .

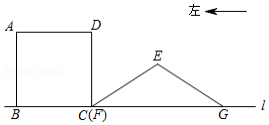
如图所示,在正方形 和 中, , ,点 、 、 、 在同一直线 上.当点 、 重合时, 以 的速度沿直线 向左开始运动, 秒后正方形 与 重合部分的面积为 .请解答下列问题:
(1)当 秒时,求 的值;
(2)当 秒时,求 的值;
(3)当5秒 秒时,求 与 的函数关系式,并求出 的最大值.
如图,正方形纸片 中,对角线 、 交于点 ,折叠正方形纸片 ,使 落在 上,点 恰好与 上的点 重合,展开后折痕 分别交 、 于点 、 ,连接 ,给出下列结论:① ;② ;③ ;④四边形 是菱形;⑤ ;⑥若 ,则正方形 的面积是 ,其中正确的结论个数为

A.2B.3C.4D.5
中, , ,点 为直线 上一动点(点 不与 , 重合),以 为边在 右侧作正方形 ,连接 .
(1)观察猜想
如图1,当点 在线段 上时,
① 与 的位置关系为: .
② , , 之间的数量关系为: ;(将结论直接写在横线上)
(2)数学思考
如图2,当点 在线段 的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)拓展延伸
如图3,当点 在线段 的延长线上时,延长 交 于点 ,连接 .若已知 , ,请求出 的长.

已知:点P是平行四边形ABCD对角线AC所在直线上的一个动点(点P不与点A、C重合),分别过点A、C向直线BD作垂线,垂足分别为点E、F,点O为AC的中点.
(1)当点P与点O重合时如图1,易证 (不需证明)
(2)直线BP绕点B逆时针方向旋转,当 时,如图2、图3的位置,猜想线段CF、AE、OE之间有怎样的数量关系?请写出你对图2、图3的猜想,并选择一种情况给予证明.

已知:点P是平行四边形ABCD对角线AC所在直线上的一个动点(点P不与点A、C重合),分别过点A、C向直线BD作垂线,垂足分别为点E、F,点O为AC的中点.
(1)当点P与点O重合时如图1,易证 (不需证明)
(2)直线BP绕点B逆时针方向旋转,当 时,如图2、图3的位置,猜想线段CF、AE、OE之间有怎样的数量关系?请写出你对图2、图3的猜想,并选择一种情况给予证明.

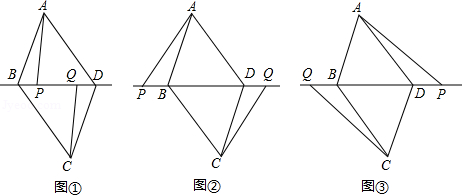
在▱ABCD中,点P和点Q是直线BD上不重合的两个动点, ,AD=BD.
(1)如图①,求证: ;
(2)请直接写出图②,图③中BP、BQ、BC三者之间的数量关系,不需要证明;
(3)在(1)和(2)的条件下,若 , ,则BC= .
如图,边长为2的正方形ABCD中,AE平分∠DAC,AE交CD于点F, ,垂足为点E, ,垂足为点G,点H在边BC上, ,连接AH、FH,FH与AC交于点M,以下结论:
① ;② ;③ ;④ ;⑤ ,
其中正确结论的个数为( )

A.2B.3C.4D.5
如图1,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.
(1)求证:△BDF是等腰三角形;
(2)如图2,过点D作DG∥BE,交BC于点G,连接FG交BD于点O.
①判断四边形BFDG的形状,并说明理由;
②若AB=6,AD=8,求FG的长.
