初中数学四边形综合题试题

（1）证明推断：如图（1），在正方形中，点，分别在边，上，于点，点，分别在边，上，．

①求证：；

②推断：的值为　　；

（2）类比探究：如图（2），在矩形中，为常数）．将矩形沿折叠，使点落在边上的点处，得到四边形，交于点，连接交于点．试探究与之间的数量关系，并说明理由；

（3）拓展应用：在（2）的条件下，连接，当时，若，，求的长．

操作体验：如图，在矩形中，点、分别在边、上，将矩形沿直线折叠，使点恰好与点重合，点落在点处．点为直线上一动点（不与、重合），过点分别作直线、的垂线，垂足分别为点和，以、为邻边构造平行四边形．

（1）如图1，求证：；

（2）特例感知：如图2，若，，当点在线段上运动时，求平行四边形的周长；

（3）类比探究：若，．

①如图3，当点在线段的延长线上运动时，试用含、的式子表示与之间的数量关系，并证明；

②如图4，当点在线段的延长线上运动时，请直接用含、的式子表示与之间的数量关系．（不要求写证明过程）

如图1，正方形和的边，在同一条直线上，且，取的中点，连接，，．

（1）试证明，并求的值．

（2）如图2，将图1中的正方形变为菱形，设，其它条件不变，问（1）中的值有变化吗？若有变化，求出该值（用含的式子表示）；若无变化，说明理由．

如图，在正方形中，，为对角线上一动点，连接，，过点作，交直线于点．点从点出发，沿着方向以每秒的速度运动，当点与点重合时，运动停止．设的面积为，点的运动时间为秒．

（1）求证：；

（2）求与之间关系的函数表达式，并写出自变量的取值范围；

（3）求面积的最大值．

如图，在正方形 $\mathit{ABCD}$ 中， $E$ 、 $F$ 分别是 $\mathit{BC}$ 、 $\mathit{CD}$ 上的点，且 $\angle \mathit{EAF}=45°$ ， $\mathit{AE}$ 、 $\mathit{AF}$ 分别交 $\mathit{BD}$ 于 $M$ 、 $N$ ，连接 $\mathit{EN}$ 、 $\mathit{EF}$ ，有以下结论：

① $\mathit{AN}=\mathit{EN}$

②当 $\mathit{AE}=\mathit{AF}$ 时， $\frac{\mathit{BE}}{\mathit{EC}}=2-\sqrt{2}$

③ $\mathit{BE}+\mathit{DF}=\mathit{EF}$

④存在点 $E$ 、 $F$ ，使得 $\mathit{NF}>\mathit{DF}$

其中正确的个数是 $($ 　　 $)$

A．

1

B．

2

C．

3

D．

4

如图，正方形 $\mathit{ABCD}$ ，点 $F$ 在边 $\mathit{AB}$ 上，且 $\mathit{AF}:\mathit{FB}=1:2$ ， $\mathit{CE}\perp \mathit{DF}$ ，垂足为 $M$ ，且交 $\mathit{AD}$ 于点 $E$ ， $\mathit{AC}$ 与 $\mathit{DF}$ 交于点 $N$ ，延长 $\mathit{CB}$ 至 $G$ ，使 $\mathit{BG}=\frac{1}{2}\mathit{BC}$ ，连接 $\mathit{GM}$ ．有如下结论：① $\mathit{DE}=\mathit{AF}$ ；② $\mathit{AN}=\frac{\sqrt{2}}{4}\mathit{AB}$ ；③ $\angle \mathit{ADF}=\angle \mathit{GMF}$ ；④ $S_{\mathit{\Delta ANF}}:S_{\mathit{四边形}\mathit{CNFB}}=1:8$ ．上述结论中，所有正确结论的序号是 $($ 　　 $)$

A．

①②

B．

①③

C．

①②③

D．

②③④

在矩形中，连结，点从点出发，以每秒1个单位的速度沿着的路径运动，运动时间为（秒．过点作于点，在矩形的内部作正方形．

（1）如图，当时，

①若点在的内部，连结、，求证：；

②当时，设正方形与的重叠部分面积为，求与的函数关系式；

（2）当，时，若直线将矩形的面积分成两部分，求的值．

如图，矩形硬纸片的顶点在轴的正半轴及原点上滑动，顶点在轴的正半轴及原点上滑动，点为的中点，，．给出下列结论：①点从点出发，到点运动至点为止，点经过的路径长为；②的面积最大值为144；③当最大时，点的坐标为，．其中正确的结论是　　．（填写序号）

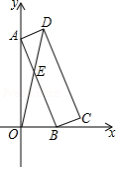
如图1，在正方形中，平分，交于点，过点作，交的延长线于点，交的延长线于点．

（1）求证：；

（2）如图2，连接、，求证：平分；

（3）如图3，连接交于点，求的值．

箭头四角形

模型规律

如图1，延长交于点，则．

因为凹四边形形似箭头，其四角具有“”这个规律，所以我们把这个模型叫做“箭头四角形”．

模型应用

（1）直接应用：①如图2，　　．

②如图3，、的2等分线（即角平分线）、交于点，已知，，则　　．

③如图4，、分别为、的2019等分线，2，3，，2017，．它们的交点从上到下依次为、、、、．已知，，则　　度．

（2）拓展应用：如图5，在四边形中，，．是四边形内一点，且．求证：四边形是菱形．

我们知道，各个角都相等，各条边都相等的多边形叫做正多边形．对一个各条边都相等的凸多边形（边数大于，可以由若干条对角线相等判定它是正多边形．例如，各条边都相等的凸四边形，若两条对角线相等，则这个四边形是正方形．

（1）已知凸五边形的各条边都相等．

①如图1，若，求证：五边形是正五边形；

②如图2，若，请判断五边形是不是正五边形，并说明理由：

（2）判断下列命题的真假．（在括号内填写“真”或“假”

如图3，已知凸六边形的各条边都相等．

①若，则六边形是正六边形；　　

②若，则六边形是正六边形．　　

定义：有两个相邻内角互余的四边形称为邻余四边形，这两个角的夹边称为邻余线．

（1）如图1，在中，，是的角平分线，，分别是，上的点．

求证：四边形是邻余四边形．

（2）如图2，在的方格纸中，，在格点上，请画出一个符合条件的邻余四边形，使是邻余线，，在格点上．

（3）如图3，在（1）的条件下，取中点，连结并延长交于点，延长交于点．若为的中点，，，求邻余线的长．

如图，正方形中，，点是对角线上一点，连接，过点作，交于点，连接，交于点，将沿翻折，得到，连接，交于点，若点是边的中点，则的周长是　　．

如图，在正方形 $\mathit{ABCD}$ 中，连接 $\mathit{AC}$ ，以点 $A$ 为圆心，适当长为半径画弧，交 $\mathit{AB}$ 、 $\mathit{AC}$ 于点 $M$ ， $N$ ，分别以 $M$ ， $N$ 为圆心，大于 $\mathit{MN}$ 长的一半为半径画弧，两弧交于点 $H$ ，连结 $\mathit{AH}$ 并延长交 $\mathit{BC}$ 于点 $E$ ，再分别以 $A$ 、 $E$ 为圆心，以大于 $\mathit{AE}$ 长的一半为半径画弧，两弧交于点 $P$ ， $Q$ ，作直线 $\mathit{PQ}$ ，分别交 $\mathit{CD}$ ， $\mathit{AC}$ ， $\mathit{AB}$ 于点 $F$ ， $G$ ， $L$ ，交 $\mathit{CB}$ 的延长线于点 $K$ ，连接 $\mathit{GE}$ ，下列结论：① $\angle \mathit{LKB}=22.5°$ ，② $\mathit{GE}//\mathit{AB}$ ，③ $\tan \angle \mathit{CGF}=\frac{\mathit{KB}}{\mathit{LB}}$ ，④ $S_{\mathit{\Delta CGE}}:S_{\mathit{\Delta CAB}}=1:4$ ．其中正确的是 $($ 　　 $)$

A．

①②③

B．

②③④

C．

①③④

D．

①②④

在平面直角坐标系中，为原点，点，点在轴的正半轴上，．矩形的顶点，，分别在，，上，．

（Ⅰ）如图①，求点的坐标；

（Ⅱ）将矩形沿轴向右平移，得到矩形，点，，，的对应点分别为，，，．设，矩形与重叠部分的面积为．

①如图②，当矩形与重叠部分为五边形时，，分别与相交于点，，试用含有的式子表示，并直接写出的取值范围；

②当时，求的取值范围（直接写出结果即可）．