我们知道,各个角都相等,各条边都相等的多边形叫做正多边形.对一个各条边都相等的凸多边形(边数大于,可以由若干条对角线相等判定它是正多边形.例如,各条边都相等的凸四边形,若两条对角线相等,则这个四边形是正方形.
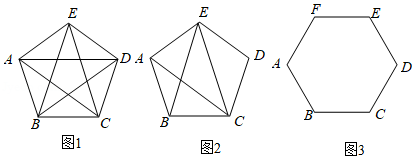
(1)已知凸五边形的各条边都相等.
①如图1,若,求证:五边形是正五边形;
②如图2,若,请判断五边形是不是正五边形,并说明理由:
(2)判断下列命题的真假.(在括号内填写“真”或“假”
如图3,已知凸六边形的各条边都相等.
①若,则六边形是正六边形;
②若,则六边形是正六边形.
相关知识点
推荐套卷
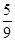 ;(3)-0.25;(4)0.13;(5)4
;(3)-0.25;(4)0.13;(5)4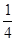 ;(6)-5
;(6)-5 ;
;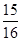 ×(-8);
×(-8); ×(8-1
×(8-1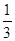 -0.04);
-0.04); 粤公网安备 44130202000953号
粤公网安备 44130202000953号