箭头四角形
模型规律
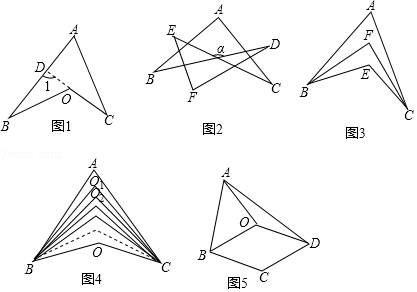
如图1，延长交于点，则．
因为凹四边形形似箭头，其四角具有“”这个规律，所以我们把这个模型叫做“箭头四角形”．
模型应用
（1）直接应用：①如图2， ．
②如图3，、的2等分线（即角平分线）、交于点，已知，，则 ．
③如图4，、分别为、的2019等分线，2，3，，2017，．它们的交点从上到下依次为、、、、．已知，，则 度．
（2）拓展应用：如图5，在四边形中，，．是四边形内一点，且．求证：四边形是菱形．
相关试题
如图，⊙O是△ACD的外接圆，AB是直径，过点D作直线DE∥AB，过点B作直线BE∥AD，两直线交于点E，∠ACD=45°，⊙O的半径是4cm.
（1）请判断DE与⊙O的位置关系，并说明理由；
（2）求图中阴影部分的面积（结果用π表示）．
÷（1+
），其中a=5-
，b=-3+
(2)、 
已知：在梯形ABCD中，CD∥AB，AD=DC=BC=2，AB=4．点M从A开始，以每秒1个单位的速度向点B运动；点N从点C出发，沿C→D→A方向，以每秒1个单位的速度向点A运动，若M、N同时出发，其中一点到达终点时，另一个点也停止运动．运动时间为t秒，过点N作NQ⊥CD交AC于点Q．
（1）设△AMQ的面积为S，求S与t的函数关系式，并写出t的取值范围．
（2）在梯形ABCD的对称轴上是否存在点P，使△PAD为直角三角形？若存在，求点P到AB的距离；若不存在，说明理由．
（3）在点M、N运动过程中，是否存在t值，使△AMQ为等腰三角形？若存在，求出t值；若不存在，说明理由．
相关知识点
推荐套卷
粤公网安备 44130202000953号