定义:有两个相邻内角互余的四边形称为邻余四边形,这两个角的夹边称为邻余线.
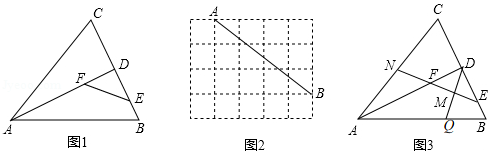
(1)如图1,在中,,是的角平分线,,分别是,上的点.
求证:四边形是邻余四边形.
(2)如图2,在的方格纸中,,在格点上,请画出一个符合条件的邻余四边形,使是邻余线,,在格点上.
(3)如图3,在(1)的条件下,取中点,连结并延长交于点,延长交于点.若为的中点,,,求邻余线的长.
推荐套卷
定义:有两个相邻内角互余的四边形称为邻余四边形,这两个角的夹边称为邻余线.
(1)如图1,在中,,是的角平分线,,分别是,上的点.
求证:四边形是邻余四边形.
(2)如图2,在的方格纸中,,在格点上,请画出一个符合条件的邻余四边形,使是邻余线,,在格点上.
(3)如图3,在(1)的条件下,取中点,连结并延长交于点,延长交于点.若为的中点,,,求邻余线的长.
