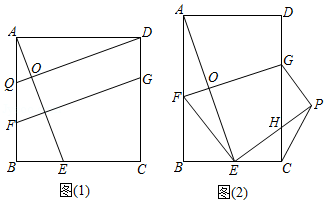
(1)证明推断:如图(1),在正方形中,点,分别在边,上,于点,点,分别在边,上,.
①求证:;
②推断:的值为 ;
(2)类比探究:如图(2),在矩形中,为常数).将矩形沿折叠,使点落在边上的点处,得到四边形,交于点,连接交于点.试探究与之间的数量关系,并说明理由;
(3)拓展应用:在(2)的条件下,连接,当时,若,,求的长.
相关知识点
推荐套卷
(1)证明推断:如图(1),在正方形中,点,分别在边,上,于点,点,分别在边,上,.
①求证:;
②推断:的值为 ;
(2)类比探究:如图(2),在矩形中,为常数).将矩形沿折叠,使点落在边上的点处,得到四边形,交于点,连接交于点.试探究与之间的数量关系,并说明理由;
(3)拓展应用:在(2)的条件下,连接,当时,若,,求的长.
