如图,平面直角坐标系中,已知点 的坐标为 .
(1)请用直尺(不带刻度)和圆规作一条直线 ,它与 轴和 轴的正半轴分别交于点 和点 ,且使 , 与 的面积相等.(作图不必写作法,但要保留作图痕迹.
(2)问:(1)中这样的直线 是否唯一?若唯一,请说明理由;若不唯一,请在图中画出所有这样的直线 ,并写出与之对应的函数表达式.
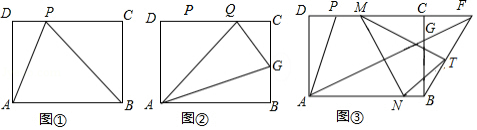
对给定的一张矩形纸片 进行如下操作:先沿 折叠,使点 落在 边上(如图① ,再沿 折叠,这时发现点 恰好与点 重合(如图②
(1)根据以上操作和发现,求 的值;
(2)将该矩形纸片展开.
①如图③,折叠该矩形纸片,使点 与点 重合,折痕与 相交于点 ,再将该矩形纸片展开.求证: ;
②不借助工具,利用图④探索一种新的折叠方法,找出与图③中位置相同的 点,要求只有一条折痕,且点 在折痕上,请简要说明折叠方法.(不需说明理由)

如图,矩形 中, 是 的中点,延长 , 交于点 ,连接 , .
(1)求证:四边形 是平行四边形;
(2)当 平分 时,写出 与 的数量关系,并说明理由.

在一次课题学习中,老师让同学们合作编题,某学习小组受赵爽弦图的启发,编写了下面这道题,请你来解一解:

如图,将矩形 的四边 、 、 、 分别延长至 、 、 、 ,使得 , ,连接 , , , .
(1)求证:四边形 为平行四边形;
(2)若矩形 是边长为1的正方形,且 , ,求 的长.
如图,已知 是矩形 的对角线.
(1)用直尺和圆规作线段 的垂直平分线,分别交 、 于 、 (保留作图痕迹,不写作法和证明).
(2)连接 , ,问四边形 是什么四边形?请说明理由.

如图,矩形 中, ,将矩形 绕点 旋转得到矩形 ,使点 的对应点 落在 上, 交 于点 ,在 上取点 ,使 .
(1)求证: .
(2)求 的度数.
(3)已知 ,求 的长.

如图,矩形 在平面直角坐标系的第一象限内, 与 轴平行, ,点 的坐标为 , 是 的中点;反比例函数 图象经过点 和点 ,过点 的直线 与反比例函数图象交于点 ,点 的纵坐标为4.
(1)求反比例函数的解析式和点 的坐标;
(2)求直线 的解析式;
(3)直接写出 时,自变量 的取值范围.

如图,点 、 分别是矩形 的边 、 上一点,若 ,且 .
(1)求证:点 为 的中点;
(2)延长 与 的延长线相交于点 ,连接 ,已知 ,求 的值.

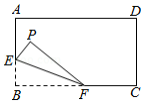
如图,将矩形 沿 折叠,使点 落在 边上的点 处,过点 作 交 于点 ,连接 .
(1)求证:四边形 是菱形;
(2)探究线段 、 、 之间的数量关系,并说明理由;
(3)若 , ,求 的长.

在现实生活中,我们经常会看到许多“标准”的矩形,如我们的课本封面、 的打印纸等,其实这些矩形的长与宽之比都为 ,我们不妨就把这样的矩形称为“标准矩形”,在“标准矩形” 中, 为 边上一定点,且 ,如图所示.
(1)如图①,求证: ;
(2)如图②,点 在 上,且 ,若 为 边上一动点,当 的周长最小时,求 的值;
(3)如图③,已知 ,在(2)的条件下,连接 并延长交 的延长线于点 ,连接 , 为 的中点, 、 分别为线段 与 上的动点,且始终保持 ,请证明: 的面积 为定值,并求出这个定值.
如图,将矩形 沿对角线 翻折,点 落在点 处, 交 于 .
(1)求证: ;
(2)若 , ,求图中阴影部分的面积.

如图,矩形 中, , , 是 上一点,且 , 是 上一动点,若将 沿 对折后,点 落在点 处,则点 到点 的最短距离为 .
如图,四边形 是矩形, , ,以 为一边向矩形外部作等腰直角 , .点 在线段 上,且 ,点 沿折线 运动,点 沿折线 运动(与点 不重合),在运动过程中始终保持线段 .设 与 之间的距离为 .
(1)若 .
①如图1,当点 在线段 上时,若四边形 的面积为48,则 的值为 ;
②在运动过程中,求四边形 的最大面积;
(2)如图2,若点 在线段 上时,要使四边形 的面积始终不小于50,求 的取值范围.

如图①是一张矩形纸片,按以下步骤进行操作:
(Ⅰ)将矩形纸片沿 折叠,使点 落在 边上点 处,如图②;
(Ⅱ)在第一次折叠的基础上,过点 再次折叠,使得点 落在边 上点 处,如图③,两次折痕交于点 ;
(Ⅲ)展开纸片,分别连接 、 、 、 ,如图④.
(探究)
(1)证明: ;
(2)若 ,设 为 , 为 ,求 关于 的关系式.
