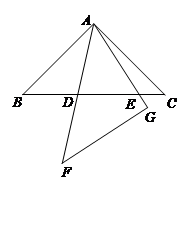
在现实生活中,我们经常会看到许多“标准”的矩形,如我们的课本封面、 的打印纸等,其实这些矩形的长与宽之比都为 ,我们不妨就把这样的矩形称为“标准矩形”,在“标准矩形” 中, 为 边上一定点,且 ,如图所示.

(1)如图①,求证: ;
(2)如图②,点 在 上,且 ,若 为 边上一动点,当 的周长最小时,求 的值;
(3)如图③,已知 ,在(2)的条件下,连接 并延长交 的延长线于点 ,连接 , 为 的中点, 、 分别为线段 与 上的动点,且始终保持 ,请证明: 的面积 为定值,并求出这个定值.
推荐套卷
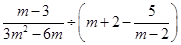 ,其中m是方程
,其中m是方程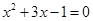 的根.
的根.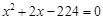
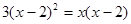
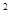 +CE
+CE
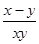 的值.
的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号