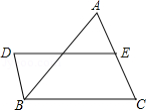
如图,在 中, , ,以线段 为边向外作等边 ,点 是线段 的中点,连接 并延长交线段 于点 .
(1)求证:四边形 为平行四边形;
(2)若 ,求平行四边形 的面积.

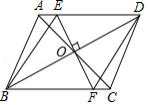
如图,已知四边形 中,对角线 、 相交于点 ,且 , ,过 点作 ,分别交 、 于点 、 .
(1)求证: ;
(2)判断四边形 的形状,并说明理由.
已知:如图,在四边形 中, ,点 为 边上一点, 与 分别为 和 的平分线.
(1)请你添加一个适当的条件 ,使得四边形 是平行四边形,并证明你的结论;
(2)作线段 的垂直平分线交 于点 ,并以 为直径作 (要求:尺规作图,保留作图痕迹,不写作法);
(3)在(2)的条件下, 交边 于点 ,连接 ,交 于点 ,若 , ,求 的半径.

如图, 已知四边形 是菱形, 于点 , 于点 .
(1) 求证: ;
(2) 若 , ,求 的值 .

如图,在平行四边形 中, 是对角线 上的一点,过点 作 ,且 ,连接 、 、 .
(1)求证: ;
(2)若 ,求证:四边形 为菱形.

如图,已知凸五边形 的边长均相等,且 , ,则 必定满足

A. B.
C. D.以上情况均有可能
如图,在 中, 是 边上的中线, 是 的中点,过点 作 的平行线交 的延长线于点 ,连接 .
(1)求证: ;
(2)若 ,试判断四边形 的形状,并证明你的结论.

如图,在 中, ,点 , 分别是边 , 上的中点,连接 并延长至点 ,使 ,连接 、 .
(1)证明: ;
(2)当 时,试判断四边形 的形状并说明理由.

如图,四边形 中, , ,且 ,以 、 、 为边向外作正方形,其面积分别为 、 、 ,若 , ,则 的值为
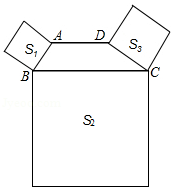
A.12B.18C.24D.48
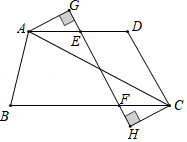
如图,四边形 中, ,点 、 分别在 、 上, ,过点 、 分别作 的垂线,垂足为 、 .
(1)求证: ;
(2)连接 ,线段 与 是否互相平分?请说明理由.
如图, ,且 , 是 的中点,
(1)求证: ;
(2)连接 、 ,若要使四边形 是矩形,则需给 添加什么条件,为什么?