初中数学平行四边形的判定与性质选择题

如图1， $▱\mathit{ABCD}$ 中， $\mathit{AD}>\mathit{AB}$ ， $\angle \mathit{ABC}$ 为锐角．要在对角线 $\mathit{BD}$ 上找点 $N$ ， $M$ ，使四边形 $\mathit{ANCM}$ 为平行四边形，现有图2中的甲、乙、丙三种方案，则正确的方案 $($ 　　 $)$

A．	甲、乙、丙都是	B．	只有甲、乙才是
C．	只有甲、丙才是	D．	只有乙、丙才是

如图，矩形 $\mathit{ABCD}$ 中， $\mathit{AC}$ ， $\mathit{BD}$ 相交于点 $O$ ，过点 $B$ 作 $\mathit{BF}\perp \mathit{AC}$ 交 $\mathit{CD}$ 于点 $F$ ，交 $\mathit{AC}$ 于点 $M$ ，过点 $D$ 作 $\mathit{DE}//\mathit{BF}$ 交 $\mathit{AB}$ 于点 $E$ ，交 $\mathit{AC}$ 于点 $N$ ，连接 $\mathit{FN}$ ， $\mathit{EM}$ ．则下列结论：

① $\mathit{DN}=\mathit{BM}$ ；

② $\mathit{EM}//\mathit{FN}$ ；

③ $\mathit{AE}=\mathit{FC}$ ；

④当 $\mathit{AO}=\mathit{AD}$ 时，四边形 $\mathit{DEBF}$ 是菱形．

其中，正确结论的个数是 $($ 　　 $)$

A．

1个

B．

2个

C．

3个

D．

4个

如图，菱形 $\mathit{ABCD}$的边长为13，对角线 $\mathit{AC}=24$，点 $E$、 $F$分别是边 $\mathit{CD}$、 $\mathit{BC}$的中点，连接 $\mathit{EF}$并延长与 $\mathit{AB}$的延长线相交于点 $G$，则 $\mathit{EG}=($　　 $)$

A．13B．10C．12D．5

如图，矩形 $\mathit{ABCD}$中， $\mathit{AD}=2$， $\mathit{AB}=3$，过点 $A$， $C$作相距为2的平行线段 $\mathit{AE}$， $\mathit{CF}$，分别交 $\mathit{CD}$， $\mathit{AB}$于点 $E$， $F$，则 $\mathit{DE}$的长是 $($　　 $)$

A． $\sqrt{5}$B． $\frac{13}{6}$C．1D． $\frac{5}{6}$

如图，点 $O$为矩形 $\mathit{ABCD}$的对称中心，点 $E$从点 $A$出发沿 $\mathit{AB}$向点 $B$运动，移动到点 $B$停止，延长 $\mathit{EO}$交 $\mathit{CD}$于点 $F$，则四边形 $\mathit{AECF}$形状的变化依次为 $($　　 $)$

A．平行四边形 $\to$正方形 $\to$平行四边形 $\to$矩形

B．平行四边形 $\to$菱形 $\to$平行四边形 $\to$矩形

C．平行四边形 $\to$正方形 $\to$菱形 $\to$矩形

D．平行四边形 $\to$菱形 $\to$正方形 $\to$矩形

如图，在 $▱\mathit{ABCD}$中，对角线 $\mathit{BD}\perp \mathit{AD}$， $\mathit{AB}=10$， $\mathit{AD}=6$， $O$为 $\mathit{BD}$的中点， $E$为边 $\mathit{AB}$上一点，直线 $\mathit{EO}$交 $\mathit{CD}$于点 $F$，连结 $\mathit{DE}$， $\mathit{BF}$．下列结论不成立的是 $($　　 $)$

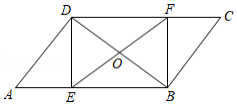
A．四边形 $\mathit{DEBF}$为平行四边形

B．若 $\mathit{AE}=3.6$，则四边形 $\mathit{DEBF}$为矩形

C．若 $\mathit{AE}=5$，则四边形 $\mathit{DEBF}$为菱形

D．若 $\mathit{AE}=4.8$，则四边形 $\mathit{DEBF}$为正方形

如图，在 $\mathit{\Delta ABC}$中，延长 $\mathit{BC}$至 $D$，使得 $\mathit{CD}=\frac{1}{2}\mathit{BC}$，过 $\mathit{AC}$中点 $E$作 $\mathit{EF}//\mathit{CD}$（点 $F$位于点 $E$右侧），且 $\mathit{EF}=2\mathit{CD}$，连接 $\mathit{DF}$．若 $\mathit{AB}=8$，则 $\mathit{DF}$的长为 $($　　 $)$

A．3B．4C． $2\sqrt{3}$D． $3\sqrt{2}$

如图，在 $\text{Rt}\Delta \text{ABC}$ 中， $\angle C=30°$ ， $D$ 、 $E$ 分别为 $\mathit{AC}$ 、 $\mathit{BC}$ 的中点， $\mathit{DE}=2$ ，过点 $B$ 作 $\mathit{BF}//\mathit{AC}$ ，交 $\mathit{DE}$ 的延长线于点 $F$ ，则四边形 $\mathit{ABFD}$ 的面积为 　　．

如图，在 $\text{Rt}\Delta \text{ABC}$中， $\angle \mathit{ACB}=90°$，以其三边为边向外作正方形，过点 $C$作 $\mathit{CR}\perp \mathit{FG}$于点 $R$，再过点 $C$作 $\mathit{PQ}\perp \mathit{CR}$分别交边 $\mathit{DE}$， $\mathit{BH}$于点 $P$， $Q$．若 $\mathit{QH}=2\mathit{PE}$， $\mathit{PQ}=15$，则 $\mathit{CR}$的长为 $($　　 $)$

A．14B．15C． $8\sqrt{3}$D． $6\sqrt{5}$

如图，在 $▱\mathit{ABCD}$中， $\mathit{CD}=2\mathit{AD}$， $\mathit{BE}\perp \mathit{AD}$于点 $E$， $F$为 $\mathit{DC}$的中点，连接 $\mathit{EF}$、 $\mathit{BF}$，下列结论：① $\angle \mathit{ABC}=2\angle \mathit{ABF}$；② $\mathit{EF}=\mathit{BF}$；③ $S_{\mathit{四边形DEBC}}=2S_{\mathit{\Delta EFB}}$；④ $\angle \mathit{CFE}=3\angle \mathit{DEF}$，其中正确结论的个数共有 $($　　 $)$

A．1个B．2个C．3个D．4个

如图，六边形 $\mathit{ABCDEF}$的内角都相等， $\angle \mathit{DAB}=60°$， $\mathit{AB}=\mathit{DE}$，则下列结论成立的个数是 $($　　 $)$

① $\mathit{AB}//\mathit{DE}$；② $\mathit{EF}//\mathit{AD}//\mathit{BC}$；③ $\mathit{AF}=\mathit{CD}$；④四边形 $\mathit{ACDF}$是平行四边形；⑤六边形 $\mathit{ABCDEF}$既是中心对称图形，又是轴对称图形．

A．2B．3C．4D．5

如图，点 $A$ ， $B$ 在反比例函数 $y=\frac{k}{x}(k>0,x>0)$ 的图象上， $\mathit{AC}\perp x$ 轴于点 $C$ ， $\mathit{BD}\perp x$ 轴于点 $D$ ， $\mathit{BE}\perp y$ 轴于点 $E$ ，连结 $\mathit{AE}$ ．若 $\mathit{OE}=1$ ， $\mathit{OC}=\frac{2}{3}\mathit{OD}$ ， $\mathit{AC}=\mathit{AE}$ ，则 $k$ 的值为 $($ 　　 $)$

A．

2

B．

$\frac{3\sqrt{2}}{2}$

C．

$\frac{9}{4}$

D．

$2\sqrt{2}$

如图，已知凸五边形 $\mathit{ABCDE}$的边长均相等，且 $\angle \mathit{DBE}=\angle \mathit{ABE}+\angle \mathit{CBD}$， $\mathit{AC}=1$，则 $\mathit{BD}$必定满足 $($　　 $)$

A． $\mathit{BD}<2$B． $\mathit{BD}=2$

C． $\mathit{BD}>2$D．以上情况均有可能

如图，在 $\mathit{\Delta ABC}$中， $\angle A=40°$， $\mathit{AB}=\mathit{AC}$，点 $D$在 $\mathit{AC}$边上，以 $\mathit{CB}$， $\mathit{CD}$为边作 $▱\mathit{BCDE}$，则 $\angle E$的度数为 $($　　 $)$

A． $40°$B． $50°$C． $60°$D． $70°$

如图，在 $\mathit{\Delta ABC}$中， $\mathit{DE}//\mathit{BC}$， $\angle \mathit{ADE}=\angle \mathit{EFC}$， $\mathit{AD}:\mathit{BD}=5:3$， $\mathit{CF}=6$，则 $\mathit{DE}$的长为 $($　　 $)$

A．6B．8C．10D．12