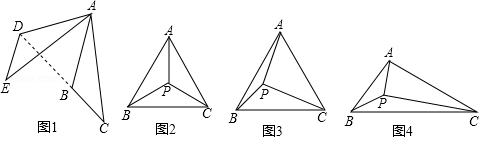
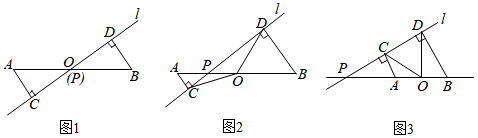
数学活动课上,某学习小组对有一内角为 的平行四边形 进行探究:将一块含 的直角三角板如图放置在平行四边形 所在平面内旋转,且 角的顶点始终与点 重合,较短的直角边和斜边所在的两直线分别交线段 , 于点 , (不包括线段的端点).
(1)初步尝试
如图1,若 ,求证:① ,② ;
(2)类比发现
如图2,若 ,过点 作 于点 ,求证: ;
(3)深入探究
如图3,若 ,探究得: 的值为常数 ,则 .

问题探究:
1.新知学习
若把将一个平面图形分为面积相等的两个部分的直线叫做该平面图形的“面线”,其“面线”被该平面图形截得的线段叫做该平面图形的“面径”(例如圆的直径就是圆的“面径”).
2.解决问题

已知等边三角形ABC的边长为2.
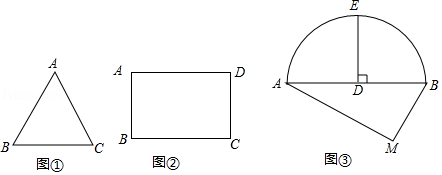
(1)如图一,若 ,垂足为D,试说明AD是△ABC的一条面径,并求AD的长;
(2)如图二,若 ,且ME是△ABC的一条面径,求面径ME的长;
(3)如图三,已知D为BC的中点,连接AD,M为AB上的一点 ,E是DC上的一点,连接ME,ME与AD交于点O,且 .
①求证:ME是△ABC的面径;
②连接AE,求证: ;
(4)请你猜测等边三角形ABC的面径长l的取值范围(直接写出结果)
(1)【操作发现】
如图1,将△ ABC绕点 A顺时针旋转60°,得到△ ADE,连接 BD,则∠ ABD= 度.
(2)【类比探究】
如图2,在等边三角形 ABC内任取一点 P,连接 PA, PB, PC,求证:以 PA, PB, PC的长为三边必能组成三角形.
(3)【解决问题】
如图3,在边长为 的等边三角形 ABC内有一点 P,∠ APC=90°,∠ BPC=120°,求△ APC的面积.
(4)【拓展应用】
如图4是 A, B, C三个村子位置的平面图,经测量 AC=4, BC=5,∠ ACB=30°, P为△ ABC内的一个动点,连接 PA, PB, PC.求 PA+ PB+ PC的最小值.
如图,抛物线 经过点 和点 与 轴的另一交点为点 ,点 是直线 上一动点,过点 作 轴,交抛物线于点 .
(1)求该抛物线的解析式;
(2)在抛物线上是否存在一点 ,使得 是等边三角形?若存在,求出点 的坐标;若不存在,请说明理由;
(3)以 为圆心, 为半径作 ,当 与坐标轴相切时,求出 的半径.

如图,在等边中,
,动点
从点
出发以
的速度沿
匀速运动.动点
同时从点
出发以同样的速度沿
的延长线方向匀速运动,当点
到达点
时,点
、
同时停止运动.设运动时间为
.过点
作
于
,连接
交
边于
.以
、
为边作平行四边形
.
(1)当为何值时,
为直角三角形;
(2)是否存在某一时刻,使点
在
的平分线上?若存在,求出
的值,若不存在,请说明理由;
(3)求的长;
(4)取线段的中点
,连接
,将
沿直线
翻折,得△
,连接
,当
为何值时,
的值最小?并求出最小值.

如图1,经过等边
的顶点
,
(圆心
在
内),分别与
,
的延长线交于点
,
,连结
,
交
于点
.
(1)求证:.
(2)当,
时,求
的长.
(3)设,
.
①求关于
的函数表达式;
②如图2,连结,
,若
的面积是
面积的10倍,求
的值.

问题提出
(1)如图①,是等边三角形,
,若点
是
的内心,则
的长为 ;
问题探究
(2)如图②,在矩形中,
,
,如果点
是
边上一点,且
,那么
边上是否存在一点
,使得线段
将矩形
的面积平分?若存在,求出
的长;若不存在,请说明理由.
问题解决
(3)某城市街角有一草坪,草坪是由草地和弦
与其所对的劣弧围成的草地组成,如图③所示.管理员王师傅在
处的水管上安装了一喷灌龙头,以后,他想只用喷灌龙头来给这块草坪浇水,并且在用喷灌龙头浇水时,既要能确保草坪的每个角落都能浇上水,又能节约用水,于是,他让喷灌龙头的转角正好等于
(即每次喷灌时喷灌龙头由
转到
,然后再转回,这样往复喷灌.
同时,再合理设计好喷灌龙头喷水的射程就可以了.
如图③,已测出,
,
的面积为
;过弦
的中点
作
交
于点
,又测得
.
请你根据以上信息,帮助王师傅计算喷灌龙头的射程至少多少米时,才能实现他的想法?为什么?(结果保留根号或精确到0.01米)
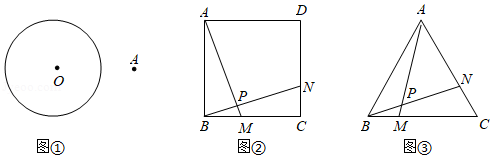
(1)如图①,点是
外一点,点
是
上一动点.若
的半径为3,且
,则点
到点
的最短距离为 ;
(2)如图②,已知正方形的边长为4,点
、
分别从点
、
同时出发,以相同的速度沿边
、
方向向终点
和
运动,连接
和
交于点
,则点
到点
的最短距离为 ;
(3)如图③,在等边中,
,点
、
分别从点
、
同时出发,以相同的速度沿边
、
方向向终点
和
运动,连接
和
交于点
,求
面积的最大值,并说明理由.
在等边 中, , ,垂足为 ,点 为 边上一点,点 为直线 上一点,连接 .
(1)将线段 绕点 逆时针旋转 得到线段 ,连接 .
①如图1,当点 与点 重合,且 的延长线过点 时,连接 ,求线段 的长;
②如图2,点 不与点 , 重合, 的延长线交 边于点 ,连接 ,求证: ;
(2)如图3,当点 为 中点时,点 为 中点,点 在边 上,且 ,点 从 中点 沿射线 运动,将线段 绕点 顺时针旋转 得到线段 ,连接 ,当 最小时,直接写出 的面积.
已知点 是线段 的中点,点 是直线 上的任意一点,分别过点 和点 作直线 的垂线,垂足分别为点 和点 .我们定义垂足与中点之间的距离为"足中距".
(1) 猜想验证 如图1,当点 与点 重合时,请你猜想、验证后直接写出"足中距" 和 的数量关系是 .
(2) 探究证明 如图2,当点 是线段 上的任意一点时,"足中距" 和 的数量关系是否依然成立,若成立,请给出证明;若不成立,请说明理由.
(3) 拓展延伸 如图3,①当点 是线段 延长线上的任意一点时,"足中距" 和 的数量关系是否依然成立,若成立,请给出证明;若不成立,请说明理由;
②若 ,请直接写出线段 、 、 之间的数量关系.
在数学兴趣小组活动中,小亮进行数学探究活动.
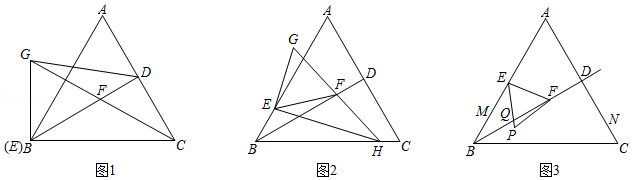
(1) 是边长为3的等边三角形, 是边 上的一点,且 ,小亮以 为边作等边三角形 ,如图1.求 的长;

(2) 是边长为3的等边三角形, 是边 上的一个动点,小亮以 为边作等边三角形 ,如图2.在点 从点 到点 的运动过程中,求点 所经过的路径长;
(3) 是边长为3的等边三角形, 是高 上的一个动点,小亮以 为边作等边三角形 ,如图3.在点 从点 到点 的运动过程中,求点 所经过的路径长;

(4)正方形 的边长为3, 是边 上的一个动点,在点 从点 到点 的运动过程中,小亮以 为顶点作正方形 ,其中点 、 都在直线 上,如图4.当点 到达点 时,点 、 、 与点 重合.则点 所经过的路径长为 ,点 所经过的路径长为 .