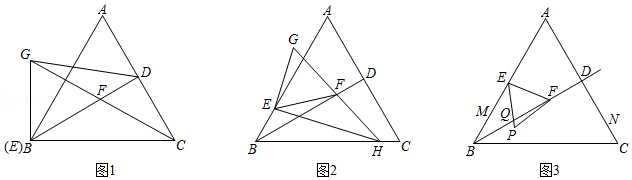
在等边 中, , ,垂足为 ,点 为 边上一点,点 为直线 上一点,连接 .
(1)将线段 绕点 逆时针旋转 得到线段 ,连接 .
①如图1,当点 与点 重合,且 的延长线过点 时,连接 ,求线段 的长;
②如图2,点 不与点 , 重合, 的延长线交 边于点 ,连接 ,求证: ;
(2)如图3,当点 为 中点时,点 为 中点,点 在边 上,且 ,点 从 中点 沿射线 运动,将线段 绕点 顺时针旋转 得到线段 ,连接 ,当 最小时,直接写出 的面积.
相关知识点
推荐套卷

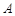 处测得电视塔尖点
处测得电视塔尖点 的仰角为
的仰角为 ,沿山坡向上走到
,沿山坡向上走到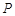 处再测得点
处再测得点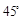 ,已知
,已知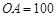 米,山坡坡度
米,山坡坡度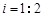 且O 、A、B在同一条直线上.求电视塔
且O 、A、B在同一条直线上.求电视塔 的高度以及此人所在位置点
的高度以及此人所在位置点
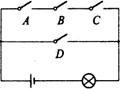
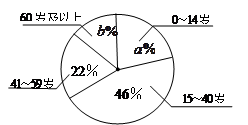

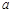 =_ ▲;
=_ ▲; 粤公网安备 44130202000953号
粤公网安备 44130202000953号