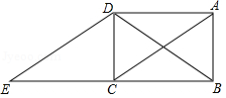
已知:在四边形 中,对角线 、 相交于点 ,且 ,作 ,垂足为点 , 与 交于点 , .
(1)如图1,求证: ;
(2)如图2, 是 的中线,若 , ,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于 面积的2倍.

如图,正方形 中, 是对角线 上的一个动点(不与 、 重合),连结 ,将 绕点 顺时针旋转 到 ,连结 交 于点 , 延长线与边 交于点 .
(1)连结 ,求证: ;
(2)若 ,求 的值;
(3)求证: .

如图,在矩形 中,连接对角线 、 ,将 沿 方向平移,使点 移到点 ,得到 .
(1)求证: ;
(2)请探究 的形状,并说明理由.
如图,四边形 中, , , ,则四边形 的面积为
A.15B.12.5C.14.5D.17
小亮在学习中遇到这样一个问题:
如图,点 是 上一动点,线段 ,点 是线段 的中点,过点 作 ,交 的延长线于点 .当 为等腰三角形时,求线段 的长度.
小亮分析发现,此问题很难通过常规的推理计算彻底解决,于是尝试结合学习函数的经验研究此问题.请将下面的探究过程补充完整:
(1)根据点 在 上的不同位置,画出相应的图形,测量线段 , , 的长度,得到下表的几组对应值.
|
0 |
1.0 |
2.0 |
3.0 |
4.0 |
5.0 |
6.0 |
7.0 |
8.0 |
|
8.0 |
7.7 |
7.2 |
6.6 |
5.9 |
|
3.9 |
2.4 |
0 |
|
8.0 |
7.4 |
6.9 |
6.5 |
6.1 |
6.0 |
6.2 |
6.7 |
8.0 |
操作中发现:
①“当点 为 的中点时, ”.则上表中 的值是 5.0 ;
②“线段 的长度无需测量即可得到”.请简要说明理由.
(2)将线段 的长度作为自变量 , 和 的长度都是 的函数,分别记为 和 ,并在平面直角坐标系 中画出了函数 的图象,如图所示.请在同一坐标系中画出函数 的图象;
(3)继续在同一坐标系中画出所需的函数图象,并结合图象直接写出:当 为等腰三角形时,线段 长度的近似值(结果保留一位小数).


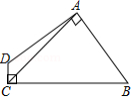
如图,在 中, ,垂足为 , ,延长 至 ,使得 ,连接 .
(1)求证: ;
(2)若 , ,求 的周长和面积.
如图,在 中, , ,点 在 的延长线上,且 ,点 在直线 上移动,过点 作射线 ,交 所在直线于点 .

(1)当点 在线段 上移动时,如图(1)所示,求证: ;
(2)当点 在直线 上移动时,如图(2)、图(3)所示,线段 与 又有怎样的数量关系?请直接写出你的猜想,不需证明.
如图为某城市部分街道示意图,四边形 为正方形,点 在对角线 上, , , ,小敏行走的路线为 ,小聪行走的路线为 .若小敏行走的路程为 ,则小聪行走的路程为 .

已知正方形 的对角线 , 相交于点 .
(1)如图1, , 分别是 , 上的点, 与 的延长线相交于点 .若 ,求证: ;
(2)如图2, 是 上的点,过点 作 ,交线段 于点 ,连接 交 于点 ,交 于点 .若 ,
①求证: ;
②当 时,求 的长.

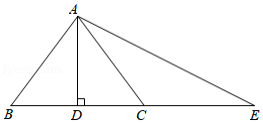
如图, 是 的边 的中点,延长 交 的延长线于点 .
(1)求证: .
(2)若 , , ,求 的长.

在 中, , ,以 为边在 的另一侧作 ,点 为射线 上任意一点,在射线 上截取 ,连接 、 、 .
(1)如图1,当点 落在线段 的延长线上时,直接写出 的度数;
(2)如图2,当点 落在线段 (不含边界)上时, 与 交于点 ,请问(1)中的结论是否仍成立?如果成立,请给出证明;如果不成立,请说明理由;
(3)在(2)的条件下,若 ,求 的最大值.

在平面直角坐标系中,已知 为等腰直角三角形, ,点 ,点 在 轴正半轴上,点 在第三象限,且在反比例函数 的图象上,则
A.3B.4C.6D.12
如图, 是 的直径, 为弦, 的平分线交 于点 ,过点 的切线交 的延长线于点 .
求证:(1) ;
(2) .
