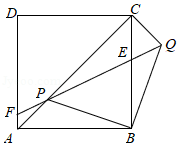
如图,正方形 中, 是对角线 上的一个动点(不与 、 重合),连结 ,将 绕点 顺时针旋转 到 ,连结 交 于点 , 延长线与边 交于点 .
(1)连结 ,求证: ;
(2)若 ,求 的值;
(3)求证: .
相关知识点
推荐套卷
如图,正方形 中, 是对角线 上的一个动点(不与 、 重合),连结 ,将 绕点 顺时针旋转 到 ,连结 交 于点 , 延长线与边 交于点 .
(1)连结 ,求证: ;
(2)若 ,求 的值;
(3)求证: .
