我们发现,用不同的方式表示同一图形的面积可以解决线段长度之间关系的有关问题这种方法称为等面积法,这是一种重要的数学方法.请你用等面积法来探究下列两个问题: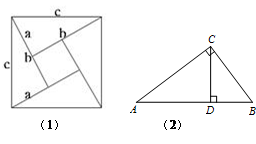
(1)如图1是著名的赵爽弦图,由四个全等的直角三角形拼成,请你用它来验证勾股定理;
(2)如图2,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,AC= 4,BC=3,求CD的长度.
推荐套卷
我们发现,用不同的方式表示同一图形的面积可以解决线段长度之间关系的有关问题这种方法称为等面积法,这是一种重要的数学方法.请你用等面积法来探究下列两个问题:
(1)如图1是著名的赵爽弦图,由四个全等的直角三角形拼成,请你用它来验证勾股定理;
(2)如图2,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,AC= 4,BC=3,求CD的长度.