在 中， ， ，以 为边在 的另一侧作 ，点 为射线 上任意一点，在射线 上截取 ，连接 、 、 ．
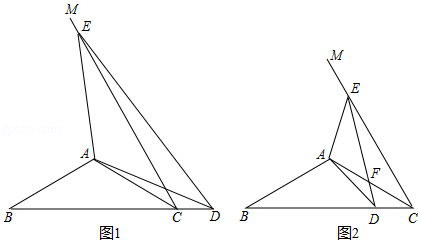
（1）如图1，当点 落在线段 的延长线上时，直接写出 的度数；
（2）如图2，当点 落在线段 （不含边界）上时， 与 交于点 ，请问（1）中的结论是否仍成立？如果成立，请给出证明；如果不成立，请说明理由；
（3）在（2）的条件下，若 ，求 的最大值．
如图，在等边△ABC中，点D在直线BC上，连接AD，作∠ADN=60°，直线DN交射线AB于点E，过点C作CF∥AB交直线DN于点F．
（1）当点D在线段BC上，∠NDB为锐角时，如图①，求证：CF+BE=CD；
（提示：过点F作FM∥BC交射线AB于点M．）
（2）当点D在线段BC的延长线上，∠NDB为锐角时，如图②；当点D在线段CB的延长线上，∠NDB为钝角时，如图③，请分别写出线段CF，BE，CD之间的数量关系，不需要证明；
（3）在（2）的条件下，若∠ADC=30°，S△ABC=4
，则BE= ，CD= ．
快、慢两车分别从相距480千米路程的甲、乙两地同时出发，匀速行驶，先相向而行，途中慢车因故停留1小时，然后以原速继续向甲地行驶，到达甲地后停止行驶；快车到达乙地后，立即按原路原速返回甲地（快车掉头的时间忽略不计），快、慢两车距乙地的路程y（千米）与所用时间x（小时）之间的函数图象如图，请结合图象信息解答下列问题：
（1）直接写出慢车的行驶速度和a的值；
（2）快车与慢车第一次相遇时，距离甲地的路程是多少千米？
（3）两车出发后几小时相距的路程为200千米？请直接写出答案．
某校为了了解本校九年级学生的视力情况（视力情况分为：不近视，轻度近视，中度近视，重度近视），随机对九年级的部分学生进行了抽样调查，将调查结果进行整理后，绘制了如下不完整的统计图，其中不近视与重度近视人数的和是中度近视人数的2倍．
请你根据以上信息解答下列问题：
（1）求本次调查的学生人数；
（2）补全条形统计图，在扇形统计图中，“不近视”对应扇形的圆心角度数是 144 度；
（3）若该校九年级学生有1050人，请你估计该校九年级近视（包括轻度近视，中度近视，重度近视）的学生大约有多少人．
在△ABC中，AB=AC=5，BC=6，以AC为一边作正方形ACDE，过点D作DF⊥BC交直线BC于点F，连接AF，请你画出图形，直接写出AF的长，并画出体现解法的辅助线．
，
）．
粤公网安备 44130202000953号