如图,直角 中, 为直角, , .点 , , 分别在 , , 边上同时开始作匀速运动,2秒后三个点同时停止运动,点 由点 出发以每秒3个单位的速度向点 运动,点 由点 出发以每秒5个单位的速度向点 运动,点 由点 出发以每秒4个单位的速度向点 运动,在运动过程中:
(1)求证: , , 的面积相等;
(2)求 面积的最小值;
(3)用 (秒 表示运动时间,是否存在 ,使 ?若存在,请直接写出 的值;若不存在,请说明理由.

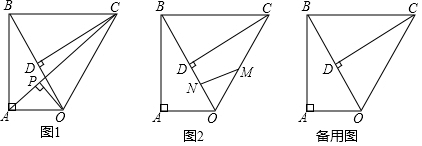
已知: 是等腰直角三角形, ,将 绕点 顺时针方向旋转得到△ ,记旋转角为 ,当 时,作 ,垂足为 , 与 交于点 .

(1)如图1,当 时,作 的平分线 交 于点 .
①写出旋转角 的度数;
②求证: ;
(2)如图2,在(1)的条件下,设 是直线 上的一个动点,连接 , ,若 ,求线段 的最小值.(结果保留根号)
已知,在 中, , , , 是 边上的一个动点,将 沿 所在直线折叠,使点 落在点 处.

(1)如图1,若点 是 中点,连接 .
①写出 , 的长;
②求证:四边形 是平行四边形.
(2)如图2,若 ,过点 作 交 的延长线于点 ,求 的长.
以菱形 的对角线交点 为坐标原点, 所在的直线为 轴,已知 , , , 为折线 上一动点,作 轴于点 ,设点 的纵坐标为 .
(1)求 边所在直线的解析式;
(2)设 ,求 关于 的函数关系式;
(3)当 为直角三角形时,求点 的坐标.

问题探究:
1.新知学习
若把将一个平面图形分为面积相等的两个部分的直线叫做该平面图形的“面线”,其“面线”被该平面图形截得的线段叫做该平面图形的“面径”(例如圆的直径就是圆的“面径”).
2.解决问题

已知等边三角形ABC的边长为2.
(1)如图一,若 ,垂足为D,试说明AD是△ABC的一条面径,并求AD的长;
(2)如图二,若 ,且ME是△ABC的一条面径,求面径ME的长;
(3)如图三,已知D为BC的中点,连接AD,M为AB上的一点 ,E是DC上的一点,连接ME,ME与AD交于点O,且 .
①求证:ME是△ABC的面径;
②连接AE,求证: ;
(4)请你猜测等边三角形ABC的面径长l的取值范围(直接写出结果)
如图1,在平面直角坐标系中,抛物线 y= x 2+ x﹣ 与 x轴交于点 A、 B(点 A在点 B右侧),点 D为抛物线的顶点,点 C在 y轴的正半轴上, CD交 x轴于点 F,△ CAD绕点 C顺时针旋转得到△ CFE,点 A恰好旋转到点 F,连接 BE.
(1)求点 A、 B、 D的坐标;
(2)求证:四边形 BFCE是平行四边形;
(3)如图2,过顶点 D作 DD 1⊥ x轴于点 D 1,点 P是抛物线上一动点,过点 P作 PM⊥ x轴,点 M为垂足,使得△ PAM与△ DD 1 A相似(不含全等).
①求出一个满足以上条件的点 P的横坐标;
②直接回答这样的点 P共有几个?

已知Rt△ OAB,∠ OAB=90°,∠ ABO=30°,斜边 OB=4,将Rt△ OAB绕点 O顺时针旋转60°,如图1,连接 BC.
(1)填空:∠ OBC= °;
(2)如图1,连接 AC,作 OP⊥ AC,垂足为 P,求 OP的长度;
(3)如图2,点 M, N同时从点 O出发,在△ OCB边上运动, M沿 O→ C→ B路径匀速运动, N沿 O→ B→ C路径匀速运动,当两点相遇时运动停止,已知点 M的运动速度为1.5单位/秒,点 N的运动速度为1单位/秒,设运动时间为 x秒,△ OMN的面积为 y,求当 x为何值时 y取得最大值?最大值为多少?
如图,在四边形 ABCD中,∠ B=60°,∠ D=30°, AB= BC.
(1)求∠ A+∠ C的度数;
(2)连接 BD,探究 AD, BD, CD三者之间的数量关系,并说明理由;
(3)若 AB=1,点 E在四边形 ABCD内部运动,且满足 AE 2= BE 2+ CE 2,求点 E运动路径的长度.

【问题】
如图1,在Rt△ ABC中,∠ ACB=90°, AC= BC,过点 C作直线 l平行于 AB.∠ EDF=90°,点 D在直线 l上移动,角的一边 DE始终经过点 B,另一边 DF与 AC交于点 P,研究 DP和 DB的数量关系.
【探究发现】
(1)如图2,某数学兴趣小组运用"从特殊到一般"的数学思想,发现当点 D移动到使点 P与点 C重合时,通过推理就可以得到 DP= DB,请写出证明过程;
【数学思考】
(2)如图3,若点 P是 AC上的任意一点(不含端点 A、 C),受(1)的启发,这个小组过点 D作 DG⊥ CD交 BC于点 G,就可以证明 DP= DB,请完成证明过程;
【拓展引申】
(3)如图4,在(1)的条件下, M是 AB边上任意一点(不含端点 A、 B), N是射线 BD上一点,且 AM= BN,连接 MN与 BC交于点 Q,这个数学兴趣小组经过多次取 M点反复进行实验,发现点 M在某一位置时 BQ的值最大.若 AC= BC=4,请你直接写出 BQ的最大值.

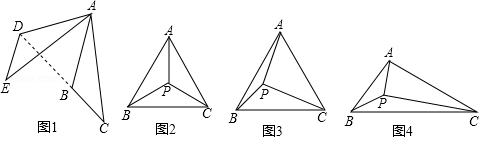
(1)【操作发现】
如图1,将△ ABC绕点 A顺时针旋转60°,得到△ ADE,连接 BD,则∠ ABD= 度.
(2)【类比探究】
如图2,在等边三角形 ABC内任取一点 P,连接 PA, PB, PC,求证:以 PA, PB, PC的长为三边必能组成三角形.
(3)【解决问题】
如图3,在边长为 的等边三角形 ABC内有一点 P,∠ APC=90°,∠ BPC=120°,求△ APC的面积.
(4)【拓展应用】
如图4是 A, B, C三个村子位置的平面图,经测量 AC=4, BC=5,∠ ACB=30°, P为△ ABC内的一个动点,连接 PA, PB, PC.求 PA+ PB+ PC的最小值.
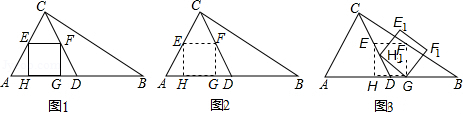
如图1,在△ ABC中,∠ ACB=90°,∠ B=30°, AC=4, D是 AB的中点, EF是△ ACD的中位线,矩形 EFGH的顶点都在△ ACD的边上.
(1)求线段 EF、 FG的长;
(2)如图2,将矩形 EFGH沿 AB向右平移,点 F落在 BC上时停止移动,设矩形移动的距离为 x,矩形与△ CBD重叠部分的面积为 S,求出 S关于 x的函数解析式;
(3)如图3,矩形 EFGH平移停止后,再绕点 G按顺时针方向旋转,当点 H落在 CD边上时停止旋转,此时矩形记作 E 1 F 1 GH 1,设旋转角为α,求cosα的值.
【问题情景】
利用三角形的面积相等来求解的方法是一种常见的等积法,此方法是我们解决几何问题的途径之一.
例如:张老师给小聪提出这样一个问题:
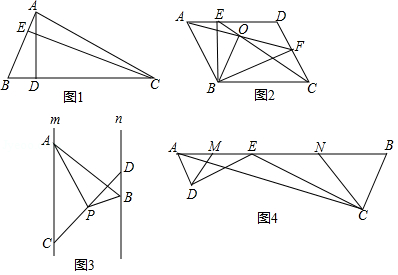
如图1,在△ ABC中, AB=3, BC=6,问△ ABC的高 AD与 CE的比是多少?
小聪的计算思路是:
根据题意得: S △ ABC= BC• AD= AB• CE.
从而得2 AD= CE,∴ =
请运用上述材料中所积累的经验和方法解决下列问题:
(1)【类比探究】
如图2,在▱ ABCD中,点 E、 F分别在 AD, CD上,且 AF= CE,并相交于点 O,连接 BE、 BF,
求证: BO平分角 AOC.
(2)【探究延伸】
如图3,已知直线 m∥ n,点 A、 C是直线 m上两点,点 B、 D是直线 n上两点,点 P是线段 CD中点,且∠ APB=90°,两平行线 m、 n间的距离为4.求证: PA• PB=2 AB.
(3)【迁移应用】
如图4, E为 AB边上一点, ED⊥ AD, CE⊥ CB,垂足分别为 D, C,∠ DAB=∠ B, AB= , BC=2, AC= ,又已知 M、 N分别为 AE、 BE的中点,连接 DM、 CN.求△ DEM与△ CEN的周长之和.
如图, 和
和 是有公共顶点的等腰直角三角形,
是有公共顶点的等腰直角三角形, ,点
,点 为射线
为射线 ,
, 的交点.
的交点.
(1)求证: ;
;
(2)若 ,
, ,把
,把 绕点
绕点 旋转,
旋转,
①当 时,求
时,求 的长;
的长;
②直接写出旋转过程中线段 长的最小值与最大值.
长的最小值与最大值.

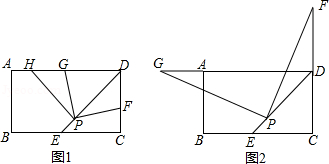
已知在矩形 中,
中, 的平分线
的平分线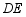 与
与 边所在的直线交于点
边所在的直线交于点 ,点
,点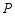 是线段
是线段 上一定点(其中
上一定点(其中
(1)如图1,若点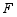 在
在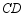 边上(不与
边上(不与 重合),将
重合),将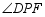 绕点
绕点 逆时针旋转
逆时针旋转 后,角的两边
后,角的两边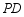 、
、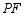 分别交射线
分别交射线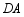 于点
于点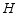 、
、 .
.
①求证: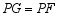 ; ②探究:
; ②探究: 、
、 、
、 之间有怎样的数量关系,并证明你的结论.
之间有怎样的数量关系,并证明你的结论.
(2)拓展:如图2,若点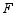 在
在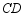 的延长线上(不与
的延长线上(不与 重合),过点
重合),过点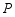 作
作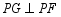 ,交射线
,交射线 于点
于点 ,你认为(1)中
,你认为(1)中 、
、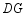 、
、 之间的数量关系是否仍然成立?若成立,给出证明;若不成立,请写出它们所满足的数量关系式,并说明理由.
之间的数量关系是否仍然成立?若成立,给出证明;若不成立,请写出它们所满足的数量关系式,并说明理由.