如图, 、 、 分别是 各边的中点,连接 、 、 .
(1)求证:四边形 为平行四边形;
(2)加上条件 后,能使得四边形 为菱形,请从① ;② 平分 ;③ 这三个条件中选择1个条件填空(写序号),并加以证明.

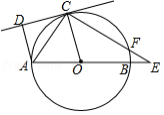
如图, AB是⊙ O的直径,弦 CD与 AB交于点 E,过点 B的切线 BP与 CD的延长线交于点 P,连接 OC, CB.
(1)求证: AE• EB= CE• ED;
(2)若⊙ O的半径为3, OE=2 BE, ,求tan∠ OBC的值及 DP的长.

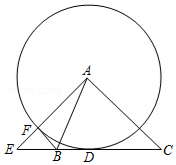
如图,在△ABC中,∠C=90°,D、F是AB边上两点,以DF为直径的⊙O与BC相交于点E,连接EF,∠OFE= ∠A.过点F作FG⊥BC于点G,交⊙O于点H,连接EH.
(1)求证:BC是⊙O的切线;
(2)连接ED,过点E作EQ⊥AB,垂足为Q,△EQD和△EGH全等吗?若全等,请予以证明;若不全等,请说明理由;
(3)当BO=5,BE=4时,求△EHG的面积.

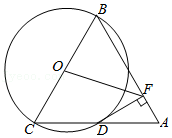
如图,已知: 是 的直径,点 在 上, 是 的切线, 于点 , 是 延长线上一点, 交 于点 ,连接 、 .
(1)求证: 平分 .
(2)若 ,
①求 的度数;
②若 的半径为 ,求线段 的长.
已知,在 中, , ,点 为 的中点.
(1)如图①,若点 、 分别为 、 上的点,且 ,求证: ;
(2)若点 、 分别为 、 延长线上的点,且 ,那么 吗?请利用图②说明理由.

如图,四边形 为平行四边形,连接 ,且 .请用尺规完成基本作图:作出 的角平分线与 交于点 .连接 交 于点 ,交 于点 ,猜想线段 和线段 的数量关系,并证明你的猜想.(尺规作图保留作图痕迹,不写作法)

如图,在 中, , 是对角线 上的两点(点 在点 左侧),且 .
(1)求证:四边形 是平行四边形;
(2)当 , , 时,求 的长.

如图,在 中, , 与 相切于点 ,过点 作 的垂线交 的延长线于点 ,交 于点 ,连结 .
(1)求证: 是 的切线.
(2)若 , ,求 的长.
如图, 为等腰直角三角形,延长 至点 使 , 是矩形,其对角线 , 交于点 ,连接 交 于点 .
(1)求证: ;
(2)求 的值.

如图,以等边三角形 的 边为直径画圆,交 于点 , 于点 ,连接 ,且 .
(1)求证: 是 的切线;
(2)求线段 的长度.
如图,在 中, , , , ,点 是边 上一点,连接 ,将 沿 翻折得到 .
(1)若 , ,且 ,求 的长;
(2)连接 ,若四边形 是平行四边形,求 与 之间的关系式.

如图,在 中, ,点 、 分别在 、 上, , 、 相交于点 .
(1)求证: ;
(2)求证: .
